Алгоритм построения детерминированного автомата из недетерминированного

 

Пусть A= (Z, X, t, z₀, F) - недетерминированный автомат.

Построим А'= (Z', X', t', z₀', F') следующим образом:

1) X'= X

2) Z'= P(Z), где P(Z) - множество некоторых подмножеств множества Z.

3) z₀'= z₀

4) F'= {"S Z| F S 0}

5) t'(S, a)= S', при этом, для "S Z, S' - это некоторое подмножество состояний P, таких, что S'={P| t(P,a)}, t(Z,a) содержит p для некоторого z S.

Построим детерминированный автомат для примера из предыдущего пункта. Множество всех подмножеств множества Z:

z₀ z₁ z₂ z_F

z₀z₁ z₀z₂ z₀z_F z₁z₂ z₁z_F z₂z_F

z₀z₁z₂ z₀z₁z_F z₀z₂z_F z₁z₂z_F

z₀z₁z₂z_F

 

Построим функцию перехода для новых состояний автомата:

 

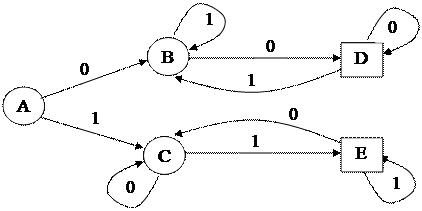
z0 (A)	z1 (B)	z2 (C)		A	B	C
z1 (B)	z1 zF (D)	z1 (B)	Þ	B	D	B
z2 (C)	z2 (C)	z2 zF (E)		C	C	E
z1 zF (D)	z1 zF (D)	z1 (B)		D	D	B
z2 zF (E)	z2 (C)	z2 zF (E)		E	C	E

 

Множество заключительных состояний F'= {D, E}