Конформные отображения.

Геометрические преобразования, при которых величины углов между любыми двумя линиями, содержащимися в преобразуемой фигуре, не изменяются, называются конформными преобразованиями или отображениями. Широкое применение конформные отображения находят в гидромеханике. Обсудим лишь общую идею метода.

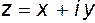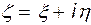Рассмотрим две координатные сетки на плоскостях комплексных переменных и (рис. 6.14).

В плоскости z имеется какая-то фигура (A), которую необходимо отобразить на плоскость . Эта операция может быть выполнена при одном непременном условии: должно быть известно соотношение, устанавливающее связь и z, т.е. 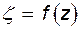. Эта зависимость носит название отображающей функции. Предположим, что она нам известна. Тогда, задавшись какой-то произвольной точкой на контуре A, например 1, можно вычислить 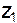, и подставив это значение в отображающую функцию, найти значение 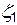и соответствующую точку на плоскости (1'). Повторив эти операции для точек 2, 3 и т.д., найдем 2', 3', ... . В результате этих действий получим контур B на плоскости , т.е. контур A отобразился в контур B. Такое преобразование получило название конформного. В теории функций комплексного переменного доказывается, что модуль производной 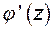характеризует изменение линейных размеров области при преобразовании, а аргумент ее определяет угол поворота радиуса-вектора. При этом преобразование, осуществляемое аналитической функцией, сохраняет эти углы во всех точках, где производная отображающей функции отличается от нуля. Теперь вопрос может быть сформулирован таким образом: какие же практические преимущества можно получить, используя метод конформных отображений?

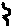
Рис. 6.14

Остановимся лишь на одном, но крайне важном случае. Как известно, одной из главных задач расчета крыля является определение его подъемной силы. Для ее нахождения необходимо знать скорости частиц в каждой точке потока, обтекающего крыло. Крыловой профиль - достаточно сложная фигура, и рассчитать скорости теоретическим путем не представляется возможным. Но, как было показано выше, расчет легко выполняется для цилиндра. Поэтому задача была бы решена, если бы удалось заменить обтекание крылового профиля обтеканием цилиндра. Это можно сделать с помощью конформного отображения.

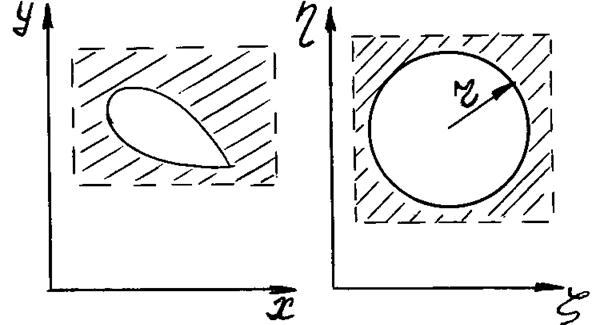
Рассмотрим рис. 6.15. Конформно отобразив фигуру, заштри­хованную на рис. 6.15а (внешность профиля) на заштрихованную фигуру рис. 6.15б (внешность окружности) мы сводим задачу обтекания профиля к задаче обтекания цилиндра. Рассчитав скорость в любой точке цилиндра, обратным переходом можно найти скорость в соответствующей ей точке профиля.

а) б)

Рис. 6.15

Нахождение вида отображающей функции, позволяющей осуществить требуемое конкретными условиями рассматриваемой задачи конформное отображение, является отдельным специальным вопросом. Решение рассмотренной выше задачи было найдено Н.Е.Жуковским. Отображающая функция в этом случае имеет вид

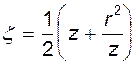(6.40)

и носит название функции Жуковского.