Аксиомы статики

В основе статики лежит несколько проверенных многовековой практикой положений, называемых аксиомами статики. Опираясь на них, логическим путем строятся все остальные положения статики.

Аксиома 1. Система двух взаимно противоположно направленных сил, равных по модулю и приложенных в одной точке, находится в равновесии (рис. 1.4).

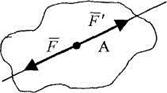
Аксиома 2. Система двух равных по модулю и противоположно направленных сил, приложенных в двух каких-либо точках абсолютно твердого тела и направленных по прямой, связывающей их точки приложения, находится в равновесии (рис. 1.5).

 

 

Рис. 1.4 Рис. 1.5

Аксиома 3. Всякую систему сил ( 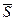₁)можно, не изменяя оказываемого ей действия, заменить другой системой сил ( 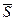₂), ей эквивалентной.

Следствие. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль линии ее действия в любую другую точку тела (рис. 1.6).

 

 

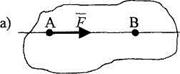
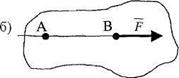
Рис. 1.6

Аксиома 4. Две системы сил, различающиеся между собой на систему сил, эквивалентную нулю, эквивалентны между собой.

Аксиома 5. (Закон параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах (рис.1.7).

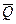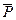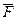Вектор , равный диагонали параллелограмма, построенного на векторах и (рис. 1.7), называется геометрической суммой этих векторов:

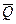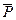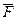= + . (1.1)

Поэтому эту аксиому можно формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.

 

 

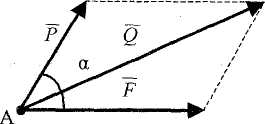
Рис. 1.7

Следствие. Любую силу можно разложить на две составляющие силы с наперед заданными линиями действия, лежащими в одной плоскости с исходной силой, точка приложения которых совпадает с точкой приложения исходной силы. В механике силу раскладывают обычно на взаимно перпендикулярные составляющие.

Аксиома 6 (3-й закон Ньютона). Две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны. Так, для точек А и В, изображенных на рис. 1.8,

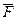₁₂ = - 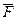_21,

где 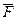₂₁ – сила, с которой точка А действует на точку В, a 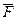₁₂ – сила, с которой точка В действует на точку А.

 

Рис. 1.8

Аксиома 7. Равновесие изменяемой механической системы (деформируемого тела), находящейся в покое, не нарушится, если систему считать неизменяемой (а тело абсолютно твердым).

Однако, следует иметь в виду, что условия равновесия системы сил, приложенных к изменяемому телу, будучи необходимыми, могут и не быть достаточными.