Проверка статистической значимости влияния полного эффекта
В двухфакторном дисперсионном анализе проверяют нулевую гипотезу (Но), утверждающую, что полный эффект (степень объединенного влияния двух факторов на зависимую переменную) не является статистически значимым.
Критерием проверки гипотезы выступает F-статистика, рассчитываемая по формуле:
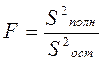 (3.17)
(3.17)
Критическое значение F-статистики (Приложение 3) зависит от числа степеней свободы в числителе и знаменателе и определяется по таблице F-распределения.
Fкрит. (  ,df1, df2)
,df1, df2)
 - уровень значимости (
- уровень значимости (  =0,05 или
=0,05 или  =0,01);
=0,01);
df1=р1р2–1 - количество степеней свободы полной дисперсии;
df2=N–p1p2 - количество степеней свободы остаточной дисперсии.
Если расчетное значение F- статистики меньше его критического значения, то в этом случае нулевую гипотезу признают верной и делают вывод о том, что полный эффект не является статистически значимым, а следовательно, не существует статистически значимых различий в средних. На этом процедуру выполнения двухфакторного дисперсионного анализа завершают.
Если расчетное значение F- статистики больше его критического значения, то в этом случае нулевую гипотезу отклоняют и делают вывод о том, что полный эффект является статистически значимым. Следует проверка следующих гипотез.