Принцип присоединения и исключения уравновешенных сил (третья аксиома)
Вторая аксиома устанавливает условие равновесия двух сил.
Две равные между собой силы ( 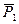 =
= 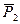 ), приложенные к абсолютно твердому телу и направленные по одной прямой в противоположные стороны, взаимно уравновешиваются (рис.3, а).
), приложенные к абсолютно твердому телу и направленные по одной прямой в противоположные стороны, взаимно уравновешиваются (рис.3, а).
Третья аксиома служит основой для преобразования систем сил.
Не нарушая равновесия абсолютно твердого тела, к нему можно приложить или отбросить от него уравновешенную систему сил.
Пусть тело (рис. 3, б) находится в состоянии равновесия. Если к нему приложить несколько взаимно уравновешенных сил 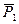 =
= 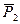 ,
, 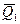 =
= 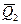 ,
, 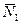 =
= 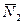 , то равновесие тела не нарушится. Аналогичный эффект получится при отбрасывании этих уравновешенных сил. Системы сил, показанные на рис. 3, а, б, эквивалентны, так как они дают одинаковый эффект– под действием каждой из них тело находится в равновесии.
, то равновесие тела не нарушится. Аналогичный эффект получится при отбрасывании этих уравновешенных сил. Системы сил, показанные на рис. 3, а, б, эквивалентны, так как они дают одинаковый эффект– под действием каждой из них тело находится в равновесии.
Из второй аксиомы вытекает следствие, согласно которому всякую силу, действующую на абсолютно твердое тело, можно перенести вдоль линии ее действия в любую точку тела, не нарушив при этом его равновесие.
Действительно, пусть на тело в точке А действует сила 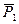 (рис. 3, в). В произвольной точке В на линии действия силы
(рис. 3, в). В произвольной точке В на линии действия силы 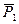 приложим две силы
приложим две силы 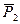 и
и 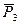 , равные по величине
, равные по величине 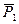 и направленные в противоположные стороны. Равновесие тела в этом случае не нарушится; отбрасывание сил
и направленные в противоположные стороны. Равновесие тела в этом случае не нарушится; отбрасывание сил 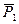 и
и 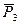 , как равных и противоположно направленных, также не нарушит равновесия. Таким образом, силу
, как равных и противоположно направленных, также не нарушит равновесия. Таким образом, силу 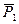 мы заменили равной силой
мы заменили равной силой 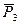 , перенесенной по линии действия
, перенесенной по линии действия 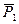 из точки А в точку В. Векторы, которые можно переносить по линии их действия, называют скользящими. Как показано выше, сила является скользящим вектором. Необходимо подчеркнуть, что перенос силы по линии ее действия возможен только в том случае, когда тела рассматриваются как абсолютно твердые. При других предпосылках это невозможно.
из точки А в точку В. Векторы, которые можно переносить по линии их действия, называют скользящими. Как показано выше, сила является скользящим вектором. Необходимо подчеркнуть, что перенос силы по линии ее действия возможен только в том случае, когда тела рассматриваются как абсолютно твердые. При других предпосылках это невозможно.
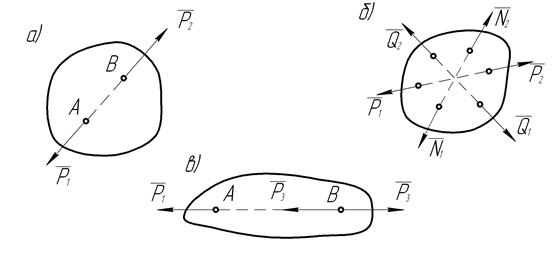
Рис. 3 .Уравновешенные системы сил.