Вычисление статистических показателей большой выборки с использованием начальных моментов
При числе единиц наблюдений 30 и более данные целесообразно свести в вариационный ряд, который можно обработать, вычислив начальные моменты. Расчет статистических показателей приведен на примере ряда распределения деревьев по 2-сантиметровым ступеням толщины (табл. 4.6).
В 3-й графе ступени толщины нумеруются от нуля – условной середины вариационного ряда – в сторону увеличения диаметра с плюсом, а уменьшения – с минусом 1, 2, 3 и т. д.
Цифры в графе 4 получаются перемножением цифр графы 2-й и 3-й, а в 5-й – перемножением цифр из 3-й и 4-й граф.
После составления таблицы вычисляются первый и второй начальные моменты, а затем статистические показатели.
Таблица 4.6
Исходные данные и начало вычисления статистических показателей вариационного ряда диаметра деревьев
| Диаметр,см (xi) | Число деревьев, шт. (ni) | ki | ni ki | ni ki2 | ni ki3 | ni ki4 |
| -4 | -4 | -64 | ||||
| -3 | -39 | -351 | ||||
| -2 | -52 | -208 | ||||
| -1 | -29 | -29 | ||||
| +1 | +24 | |||||
| +2 | +38 | |||||
| +3 | +30 | |||||
| +4 | +8 | |||||
| Итого | - | -24 | -76 |
Первый начальный момент (m1):
m1 = 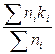 =
= 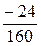 = - 0,15.
= - 0,15.
Второй начальный момент (m2):
m2 = 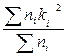 =
= 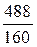 = 3,05.
= 3,05.
Аналогично рассчитаем начальные моменты m3 и m4 :
m3 =  =
=  = – 0,48; m4 =
= – 0,48; m4 = 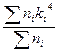 =
=  = 21,28.
= 21,28.
Среднее значение (М):
М =х0 + m1i = 14 +(-0,15·2) = 14 – 0,30 = 13,7 (см),
где i – интервал между ступенями толщины (равен 2 см).
Среднеквадратическое отклонение ( 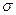 ):
):
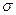 =
=  i
i 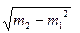 =
=  2
2 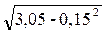 =
=  2
2 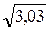 =
=  2· 1,74 =
2· 1,74 =  3,48 (см).
3,48 (см).
Коэффициент варьирования (V):
V =  100 =
100 =  100 = 25,4 (%).
100 = 25,4 (%).
Ошибка среднего значения (mM):
mM = 
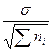 =
= 
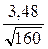 =
= 
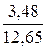
 =
=  0,28 (см).
0,28 (см).
Точность опыта (Р):
Р = 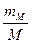 100 =
100 =  100 = 2,1 (%).
100 = 2,1 (%).
Достоверность среднего значения (t1):
t1 =  =
= 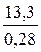 = 47,5 (достоверно, так как >4).
= 47,5 (достоверно, так как >4).