СЛУЧАЙНЫЕ ПОГРЕШНОСТИ. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ РЕЗУЛЬТАТОВ И ПОГРЕШНОСТЕЙ

 

Когда при проведении с одинаковой тщательностью и в одинаковых условиях повторных наблюдений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Каждая такая погрешность возникает вследствие одновременного воздействия на результат наблюдения многих случайных возмущений и сама является случайной величиной. В этом случае предсказать результат отдельного наблюдения и исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится Һ пределах разброса результатов наблюдений от Xmin до Xmax, где Xmin, Xmax — соответственно, нижняя и верхняя границы разброса. Однако остается неясным, какова вероятность появления того или иного значения погрешности, какое из множества лежащих в этой области значений величины принять за результат измерения и какими показателями охарактеризовать случайную погрешность результата. Для ответа на эти вопросы требуется принципиально иной, чем при анализе систематических погрешностей, подход. Подход этот основывается на рассмотрении результатов наблюдений, результатов измерений и случайных погрешностей как случайных величин. Методы теории вероятностей и математической статистики позволяют установить вероятностные (статистические) закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его случайной погрешности.

Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма — закон распределения плотности вероятностей случайной величины.

Рассмотрим формирование дифференциального закона на примере измерений с многократными наблюдениями. Пусть произведено n последовательных наблюдений одной и той же величины х и получена группа наблюдений x₁, х₂, х₃,..., х_n. Каждое из значений хi, содержит ту или иную случайную погрешность. Расположим результаты наблюдений в порядке их возрастания, от Xmin до Xmax и найдем размах ряда L = Xmax - Xmin. Разделив размах ряда на к равных интервалов ∆l = L/k, подсчитаем количество наблюдений n_к, попадающих в каждый интервал. Изобразим полученные результаты графически, нанеся на оси абсцисс значения физической величины и обозначив границы интервалов, а по оси ординат — относительную частоту попаданий n_к / n . Построив на диаграмме прямоугольники, основанием которых является ширина интервалов, а высотой n_к / n, получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте.

 

рис. 2.4 Гистограмма

 

На рис. 2.4 показана полученная в одном из опытов гистограмма, построенная на основании результатов 5( наблюдений, сгруппированных в табл. 2.1.

Таблица 2,1

 

В данном опыте в первый и последующие интервалы попадает соответственно 0,1; 0,2; 0,36; 0,22 и 0,12 от общего количества наблюдений при этом очевидно, что сумма этих чисел равна единице.

Если распределение случайной величины х статистически устойчиво то можно ожидать, что при повторных сериях наблюдений той же величины, в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Это означает, что единожды построив гистограмму, при последующих сериях наблюдений можно с определенной долей уверенности заранее предсказать распределение результатов наблюдений по интервалам. Приняв общую площадь, ограниченную контуром гистограммы и осью абсцисс, за единицу, S₀ = 1 относительную частоту попаданий результатов наблюдений в тот или иной интервал можно определить, как отношение площади соответствующего прямоугольника шириной ∆l к общей площади.

При бесконечном увеличении числа наблюдений n → ∞ и бесконечном уменьшении ширины интервалов ∆l → 0, ступенчатая кривая,

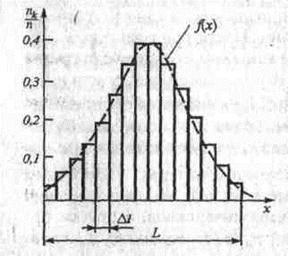
огибающая гистограмму, перейдет в плавную кривую ƒ(х) (рис. 2.5), называемую кривой платности распределения вероятностей случайной величины, а уравнение, описывающее ее, — дифференциальным законом распределения кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде

∫f(x)dx = l.

 

 

Рис. 2.5. Кривая плотности распределения вероятностей

 

Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от x1 до х2

Графически эта вероятность выражается отношением площади, лежащей под кривой f(x) в интервале от х1 до х2 к общей площади, ограниченной кривой распределения.

 

Рис. 2,6 Распределение дискретной случайной величины

 

Кроме непрерывных случайных величин в метрологической практике встречаются и дискретные случайные величины. Пример распределения дискретной случайной величины приведен на рис. 2.6.

Для описания частных свойств случайной величины используют числовые характеристики распределений. В качестве числовых характеристик выступают моменты случайных величин: начальные и центральные. Все они представляют собой некоторые средние значения; причем, если усредняются величины, отсчитываемые от начала координат, моменты называются начальными, а если от центра закона распределения—то центральными.

Начальный момент k-то порядка определяется формулами

где р_i - вероятность появления дискретной величины.

Здесь и ниже первая формула относится к непрерывным, а вторая к дискретным случайным величинам.

Из начальных моментов наибольший интерес представляет математическое ожидание случайной величины (к = 1),

Центральные моменты k-го порядка рассчитываются по формулам

 

 

Из центральных моментов особенно важную роль играет второй момент (к=2), дисперсия случайной величины D

 

Дисперсия случайной величины характеризует рассеяние отдельных ее значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии — средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.

Оценка результата измерения. Задача состоит в том, чтобы по полученным экспериментальным путем результатам наблюдений, содержащим случайные погрешности, найти оценку истинного значения измеряемой величины — результат измерения. Будем полагать, что систематические погрешности в результатах наблюдений отсутствуют или исключены.

К оценкам, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности. Оценка называется состоятельной, если при увеличении числа наблюдений она стремится к истинному значению оцениваемой величины.

return false">ссылка скрыта

Оценка называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемой величины. В том случае, когда можно найти несколько несмещенных оценок, лучшей из них считается та, которая имеет наименьшую дисперсию. Чем меньше дисперсия оценки, тем более эффективной считают эту оценку.

Способы нахождения оценок результата зависят от вида функции распределения и от имеющихся соглашений по этому вопросу, регламентируемых в рамках законодательной метрологии. Общие соображения по выбору оценок заключаются в следующем.

Распределения погрешностей результатов наблюдений, как правило, являются симметричными относительно центра распределения, поэтому истинное значение измеряемой величины может быть определено как координата центра рассеивания х_ц, т.е. центра симметрии распределения случайной погрешности (при условии, что систематическая погрешность исключена). Отсюда следует принятое в метрологии правило оценивания случайной погрешности в виде интервала, симметричного относительно результата измерения (х_ц +/- ∆х). Координата х_ц может быть найдена несколькими способами. Наиболее общим является определение центра метрии из принципа симметрии вероятностей, т.е. нахождение такой си на оси х, слева и справа от которой вероятности появления раз-дых значений случайных погрешностей равны между собой и составит Р, = Р2 = 0,5. Такое значение х_ц называется медианой.

Координата х_ц может быть определена и как центр тяжести распределения, т.е. как математическое ожидание случайной величины.

При ассиметричной кривой плотности распределения вероятностей оценкой центра распределения может служить абсцисса моды распределения, т.е. координата максимума плотности. Однако есть распределения, у которых не существует моды (например, равномерное), и распределения, у которых не существует математического ожидания.

. В практике измерений встречаются различные формы кривой закона распределения, однако чаще всего имеют дело с нормальным и равномерным распределением плотности вероятностей.

Учитывая многовариантность подходов к выбору оценок и в целях обеспечения единства измерений, правила обработки результатов наблюдений обычно регламентируются нормативно-техническими документами (стандартами, методическими указаниями, инструкциями). Так, в стандарте на методы обработки результатов прямых измерений с многократными наблюдениями указывается, что приведенные в нем методы обработки установлены для результатов наблюдений, принадлежащих нормальному распределению.

Нормальное распределение. Нормальное распределение плотности вероятности (рис. 2.7) характерно тем, что, согласно центральной предельной теореме теории вероятностей, такое распределение имеет сумма бесконечно большого числа бесконечно малых случайных возмущений с 'любыми распределениями. Применительно к измерениям это означает, {что нормальное распределение случайных погрешностей возникает тогда, когда на результат измерения действует множество случайных возмущений, ни одно из которых не является преобладающим. Практически, суммарное воздействие даже сравнительно небольшого числа возмущений приводит к закону распределения результатов и погрешностей измерений, близкому к нормальному.

 

Рис. 2.7. Кривые нормального распределения

 

В аналитической форме нормальный закон распределения выражается формулой

 

 

где х — случайная величина; mх — математическое ожидание случайной величины; σ — среднее квадратическое отклонение.

Перенеся начало координат в центр распределения mх и откладывая по оси абсцисс погрешность ∆х = х — mх, получим кривую нормального распределения погрешностей

 

Для группы из п наблюдений, распределенных по нормальному закон

 

Обратим внимание на несколько свойств нормального распределения погрешностей.

Кривая нормального распределения погрешностей симметрична относительно оси ординат. Это означает, что погрешности, одинаковые по величине, т.е. при большом числе наблюдений встречаются одинаково часто. Математическое ожидание случайной погрешности равно нулю.

Из характера кривой следует, что при нормальном законе распределения малые погрешности будут встречаться чаще, чем большие. Так, вероятность появления погрешностей, укладывающихся в интервал от 0 до ∆х1, характеризуемая площадью S1, будет значительно больше, чем вероятность появления погрешностей в интервале от ∆х2 до ∆х3 (площадь S2).

На рис.2,8 изображены кривые нормального распределения с различными средними квадратическими отклонениями, причем σ1> σ2> σ3.

Рис. 2,8 Рассеяние результатов наблюдений

 

Сравнивая кривые между собой можно убедиться, что чем меньше СКО, тем выше рассеяние результатов наблюдений и тем больше вероятность того, что большинство случайных погрешностей в них будет мало. Естественно заключить, что качество измерений тем выше, чем меньше СКО случайных погрешностей.

Если случайная величина х принимает значения лишь в пределах некоторого конечного интервала от х1 до х2 с постоянной плотностью вероятностей (рис. 2.9), то такое распределение называется равномерным и описывается соотношениями

 

Рис. 2,9 Равномерное распределение случайной величины

 

Так как площадь, ограниченная кривой распределения равна единице, то

 

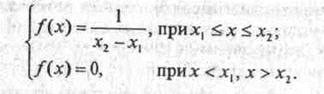
С учетом (2.11) плотность распределения

Математическое ожидание величины х

 

 

В силу симметрии равномерного распределения медиана величины х также равна (х1+х2)/2

Моды закон равномерной плотности не имеет. Дисперсия величины х определяется по формуле:

откуда СКО

Варианты оценки случайных погрешностей. Для количественной оценки случайных погрешностей и установления границ случайной по грешности результата измерения могут использоваться: предельная погрешность, интервальная оценка, числовые характеристики закона распределения. Выбор конкретной оценки определяется необходимой полнотой сведений о погрешности, назначением измерений и характером использования их результатов. Комплексы оценок показателей точности установлены стандартами.

Предельная погрешность ∆m— погрешность, больше которой в данном измерительном эксперименте не может появиться. Теоретически, такая оценка погрешности правомерна только для распределений, границы которых четко выражены и существует такое значение ±∆m, которое ограничивает возможные значения случайных погрешностей с обеих сторон от центра распределения (например, равномерное).

На практике такая оценка есть указание наибольшей погрешности, которая может встретиться при многократных измерениях одной и той же величины.

Недостатком такой оценки является то, что она не содержит информации о характере закона распределения случайных погрешностей. При арифметическом суммировании предельных погрешностей получаемая сумма может значительно превышать действительные погрешности.

Более универсальными и информативными являются квантильные оценки. Площадь, заключенная под всей кривой плотности распределения погрешностей, отражает вероятность всех возможных значений погрешности и по условиям нормирования равна единице. Эту площадь можно разделить вертикальными линиями на части. Абсциссы таких линий называются квантилями. Так, на рис. 2.10 ∆х, есть 25 %-ная квантиль, так как площадь под кривой ƒ{∆x) слева от нее составляет 25% всей площади. Абсцисса ∆х2 соответствует 75 %-ной квантили. Между ∆х, и ∆х2 заключено 50% всех возможных значений погрешности, а остальные лежат вне этого интервала.

Квантильная оценка погрешности представляется интервалом от -∆х(Р) до +∆х(Р), на котором с заданной вероятностью Р встречаются Р•100% всех возможных значений случайной погрешности. Интервал с границами ±∆х(Р) Называется доверительным интервалом случайной погрешности, а соответствующая ему вероятность — доверительной вероятностью. Принято границы доверительного интервала (доверительные границы) указывать Ірімметричными относительно результата измерения.

Так как квантили, ограничивающие доверительный интервал по
грешности могут быть выбраны различными, то при оценивании
Случайной погрешности доверительными границами необходимо одно
временно указывать значение принятой доверительной вероятности
(например, ±0,ЗВ при Р = 0,95).

Доверительные границы случайной погрешности ∆х(Р), соответствующие доверительной вероятности Р, находят по формуле

∆х(Р) = tσ,

где t — коэффициент, зависящий от Р и формы закона распределения.

На графике нормального распределения погрешностей (рис. 2.11) по оси абсцисс отложены интервалы с границами ±σ, ±2σ, ±3σ, ±4σ. Доверительные вероятности для этих интервалов приведены в табл. 2.2.

Как видно из этой таблицы, оценка случайной погрешности группы наблюдений интервалом ±1ст соответствует доверительной вероятности 0,68. Такая оценка не дает уверенности в высоком качестве измерений, поскольку 32% от всего числа наблюдений может выйти за пределы указанного интервала, что совершенно неприемлемо при однократных измерениях и дезинформирует потребителя измерительной информации. Доверительному интервалу ±3σ соответствует Р = 0,997. Это означает, что практически с вероятностью очень близкой к единице ни одно из возможных значений погрешности при нормальном законе ее распределения не выйдет за границы интервала. Поэтому, при нормальном распределении погрешностей, принято считать случайную погрешность с границами ±3σ предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируют как грубые или промахи.

 

 

Рис. 2.11 К понятию доверительных интервалов

Таблица 2.2.

 

В целях единообразия в оценивании случайных погрешностей интервальными оценками при технических измерениях доверительная вероятность принимается равной 0,95. Лишь для особо точных и ответственных измерений (важных, например, для безопасности и здоровья людей) допускается применять более высокую доверительную вероятность. -

Недостатком оценивания случайной погрешности доверительным интервалом при произвольно выбираемых доверительных вероятностях является невозможность суммирования нескольких погрешностей, так как доверительный интервал суммы не равен сумме доверительных интервалов. В то же время необходимость в суммировании случайных погрешностей существует, когда нужно оценить погрешность суммированием ее составляющих, подчиняющихся к тому же разным законам распределения.

В теории вероятностей показано, что суммирование статистически независимых случайных величин осуществляется путем суммирования их дисперсией

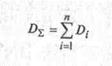
Или

 

Таким образом, для того чтобы отдельные составляющие случайной погрешности можно было суммировать расчетным путем, они должны быть представлены своими СКО, а не предельными или доверительными 'границами.

Формула (2.13) правомерна только для некоррелированных случайных величин. В том случае, когда суммируемые составляющие погрешности коррелированы, расчетные соотношения усложняются, так как требуется учет корреляционных связей. Методы выявления корреляционных связей и их учет являются предметом изучения в теории вероятностей.

Рассмотренные свойства распределений следует понимать как «идеальные», полученные на основе бесконечно большого числа опытов. В реальных условиях результат измерения получают либо путем обработки ограниченной группы наблюдений, либо на основе однократного измерения. Правила обработки данных для получения оценок результата и погрешности статистических измерений определены стандартами Государственной системы обеспечения единства измерений.