КОЛЕБАНИЯ И ВОЛНЫ
Вопросы для программированного теоретического коллоквиума по физике, 2003 г.
1.1. Ниже под номерами 2, 4, 8 приведены графики зависимости от смещения Х полной W и потенциальной Wn энергии материальной точки, а под номером 1 – модуль F результирующей силы 
, действующей на материальную точку.
Какие графики соответствуют гармоническим колебаниям материальной точки? Укажите сумму их номеров.
1.2. Материальная точка совершает незатухающие гармонические колебания вдоль оси 0х. Для нее считаются известными следующие величины:
1. х – смещение (координата) точки в произвольный момент времени t (х¹0);
2. ах – проекция на ось 0х ускорения точки в этот же момент времени;
4. W – полная механическая энергия;
8. k – жесткость системы.
Выразите массу m материальной точки через эти величины. Какие из них вошли в расчетную формулу? Укажите сумму их номеров.
1.3. Частица совершает вынужденные колебания в среде с коэффициентом затухания колебаний b. Под номером 1 приведен график зависимости амплитуды А вынужденных колебаний частицы от частоты W вынуждающей силы. Какой из трех других графиков будет соответствовать зависимости А(W), если коэффициент затухания колебаний b увеличится?
1.4. Уравнение затухающих колебаний материальной точки имеет вид
,
где А0 = 10 см, w0 = 10 рад/с.
Чему равен период Т колебаний этой точки, если коэффициент затухания колебаний b = 8 с-1?
1.5. Ниже под номерами 1 и 2 изображены траектории результирующего движения, получающегося при сложении двух взаимно перпендикулярных гармонических колебаний, а под номерами 4 и 8 – векторные диаграммы, получаемые при сложении двух гармонических колебаний одного направления и одинаковой частоты с амплитудами А1 и А2 (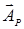 
- вектор результирующего колебания).
 |
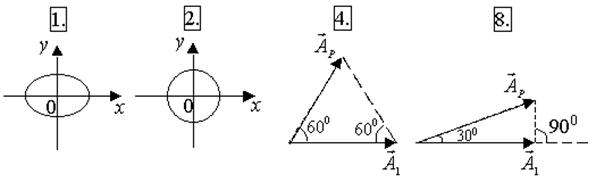Для таких случаев разность фаз Dj складываемых колебаний равна p/2? Укажите сумму их номеров.
1.6. Для каких случаев амплитуды А1 и А2 складываемых колебаний не равны друг другу (рис. из 1.5)? Укажите сумму номеров этих рисунков.
1.7. Найдите максимальную энергию Wэ max электрического поля конденсатора, если максимальное напряжение на конденсаторе колебательного контура Um=80 В, индуктивность контура L = 10-2 Гн, период колебания Т = 2p×10-3 с. сопротивлением контура пренебречь.
1.8. На рис. приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 3 с. Источник колебаний находится в точке с координатой Х = 0. В начальный момент времени t = 0 все частицы среды находились в покое. Чему равна (в СИ) скорость V распространения волны?
1.9. Чему равна (в СИ) максимальная скорость Vm частиц среды?
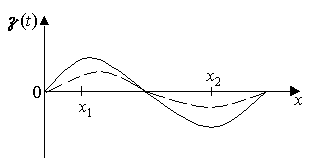1.10. На рис. приведены графики смещения частиц среды в стоячей волне для двух различных моментов времени.
Чему равна (в СИ) разность фаз Dj колебаний частиц с координатами х1 и х2?
1.11. Ниже под номерами 1, 4 изображены векторы напряженности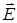 
электрического и индукции 
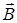магнитного полей, а под номерами 2 и 8 – вектор Умова-Пойнтинга 
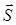плоской электромагнитной волны.
В каких случаях электромагнитная волна распространяется в положительном направлении оси 0у? Укажите сумму номеров этих диаграмм.
1.12. В среде распространяется плоская электромагнитная волна. Известны следующие параметры волны и характеристики среды:
1. e - диэлектрическая проницаемость среды,
2. m - магнитная проницаемость среды,
4. Еm – амплитуда напряженности электрического поля волны,
8. l - длина волны в среде.
Получите выражение для периода Т волны через приведенные выше величины и константы e0, m0, с. Укажите сумму номеров величин, вошедших в расчетную формулу.
1.13. Получите выражение для амплитуды Bm индукции магнитного поля волны через приведенные выше величины и константы e0, m0, с. Какие из обозначенных цифрами величин вошли в расчетную формулу? Укажите сумму их номеров.
1.14. Электрический диполь совершает гармонические колебания вдоль оси 00¢. Цифрами обозначены различные направления в пространстве. В каких направлениях энергия излучения диполя максимальна? Укажите сумму номеров этих направлений.
Составители: М.Г. Валишев, Е.С. Левин, Ф.А. Сидоренко
ã ГОУ ВПО УГТУ-УПИ, Екатеринбург, 2003.