Практические задания
1. Сторона ВС треугольника АВС разделена на пять равных частей и все точки деления  соединены с противолежащей вершиной А. Обозначив стороны
соединены с противолежащей вершиной А. Обозначив стороны  , найти выражения для векторов
, найти выражения для векторов  .
.
2. В равнобочной трапеции АВСD известно нижнее основание 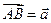 , боковая сторона
, боковая сторона  и угол между ними
и угол между ними 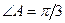 . Разложить по
. Разложить по  и
и  все векторы, составляющие остальные стороны и диагонали трапеции.
все векторы, составляющие остальные стороны и диагонали трапеции.
3. Доказать, что сумма векторов, соединяющих центр правильного треугольника с его вершинами, равна нулю.
4. В тетраэдре АВСD даны ребра, выходящие из вершины А: 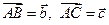 и
и  . Выразить через эти векторы остальные ребра тетраэдра а так же медиану
. Выразить через эти векторы остальные ребра тетраэдра а так же медиану  грани ВСD.
грани ВСD.
5. Найти линейную зависимость между данными четырьмя некомпланарными векторами:  ,
,  ,
,  ,
,  .
.
6. Разложить вектор 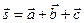 по трем некомпланарным векторам
по трем некомпланарным векторам  ,
,  ,
,  .
.
7. Зная одну из вершин треугольника А(2,-5,3) и векторы, совпадающие с двумя его сторонами 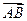 (4,1,2) и
(4,1,2) и  (3,-2,5), найти остальные вершины и сторону
(3,-2,5), найти остальные вершины и сторону  .
.
8. Доказать, что четырехугольник, все вершины которого определены своими радиус-векторами  ,
,  ,
,  ,
,  , есть параллелограмм.
, есть параллелограмм.
9. Проверить, что треугольник с вершинами  ,
,  ,
,  – прямоугольный.
– прямоугольный.
10. Найти единичный вектор  , одновременно перпендикулярный к вектору
, одновременно перпендикулярный к вектору  и к оси абсцисс.
и к оси абсцисс.
11. Даны компоненты трех сил  ;
; 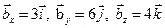 ;
;  . Найти величину и направление равнодействующей силы
. Найти величину и направление равнодействующей силы  .
.
12. Зная векторы, совпадающие с двумя сторонами треугольника 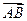 (2,1,-2) и
(2,1,-2) и  (3,2,6) вычислить углы этого треугольника, а также его площадь.
(3,2,6) вычислить углы этого треугольника, а также его площадь.
13. Проверить, что радиус-вектор любой точки прямой, делящей пополам угол между  и
и  , может быть представлен формулой:
, может быть представлен формулой:  . Найти уравнение, связывающее координаты любой точки этой прямой.
. Найти уравнение, связывающее координаты любой точки этой прямой.
14. В треугольнике АВС точка О – точка пересечения медиан а точка М – середина отрезка АВ. Принимая за базисные векторы  и
и  , найти в этом базисе координаты векторов
, найти в этом базисе координаты векторов 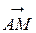 ,
,  ,
, 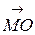 .
.
15. Три последовательных вершины трапеции АВСД находятся в точках А(-3,-2, -1), В(1,2,3), С(9,6,4). Найти четвертую вершину Д этой трапеции, зная, что длина основания  равна 15. Найти также точку М пересечения диагоналей трапеции.
равна 15. Найти также точку М пересечения диагоналей трапеции.
16. Вершина А параллелепипеда АВСД  принята за начало координат, а три ребра
принята за начало координат, а три ребра  ,
,  ,
,  – за базисные векторы. Найти в этой системе координаты всех вершин параллелепипеда.
– за базисные векторы. Найти в этой системе координаты всех вершин параллелепипеда.
17. Даны три последовательные вершины трапеции А(-2,-3), В(1,4) и С(3,1). Найти четвёртую её вершину Д при условии, что основание  в пять раз больше основания
в пять раз больше основания  . Найти также точку М пересечения диагоналей.
. Найти также точку М пересечения диагоналей.
18. Даны середины сторон треугольника (2,4), (-3, 0), (2,1). Найти его вершины.
19. Проверить, что векторы 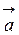 (4, 1, -1)),
(4, 1, -1)),  (1, 2, -5) и
(1, 2, -5) и  (-1, 1, 1) образуют базис в пространстве. Найти координаты вектора
(-1, 1, 1) образуют базис в пространстве. Найти координаты вектора  (4, 4, -5) в этом базисе.
(4, 4, -5) в этом базисе.
20. Проверить, что векторы 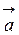 (4, 1, -1)),
(4, 1, -1)),  (1, 2, -5) и
(1, 2, -5) и  (-1, 1, 1) образуют базис в пространстве. Найти координаты вектора
(-1, 1, 1) образуют базис в пространстве. Найти координаты вектора  (2, 4, -10) в этом базисе.
(2, 4, -10) в этом базисе.
21. Дана точка А(2,4). Найти точку В при условии, что точка С пересечения прямой АВ с осью ординат делит отрезок АВ в отношении равном 2/3, а точка Д пересечения прямой АВ с осью абсцисс делит отрезок АВ в отношении -3/4.
22. Установить, являются ли векторы  , ленейно зависимыми, и в том случае когда это возможно представить вектор
, ленейно зависимыми, и в том случае когда это возможно представить вектор  как линейную комбинацию векторов
как линейную комбинацию векторов  и
и  .
.
23. Установить, являются ли векторы  , ленейно зависимыми, и в том случае когда это возможно представить вектор
, ленейно зависимыми, и в том случае когда это возможно представить вектор  как линейную комбинацию векторов
как линейную комбинацию векторов  и
и  .
.
24. Вычислить объем параллелепипеда, построенного на трех данных векторах 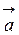 (3, 1, -2)),
(3, 1, -2)),  (-4, 0, 3) и
(-4, 0, 3) и  (1, 5, -1), и исследовать, образуют ли векторы левую или правую тройку.
(1, 5, -1), и исследовать, образуют ли векторы левую или правую тройку.
25. В плоскости (х,у) найти вектор  , перпендикулярный вектору
, перпендикулярный вектору  (5,-3,4) и имеющий одинаковую с ним длину.
(5,-3,4) и имеющий одинаковую с ним длину.
26. Показать, что точки  лежат на одной прямой, если
лежат на одной прямой, если  .
.
27. В треугольнике АВС обозначены  , выразить через
, выразить через  все медианы этого треугольника.
все медианы этого треугольника.
28. Чему равна сумма  , если
, если 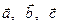 – три орта, удовлетворяющие условию
– три орта, удовлетворяющие условию  ?
?
29. Зная, что векторы 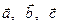 образуют треугольник, т.е.
образуют треугольник, т.е.  , вычислить длину стороны
, вычислить длину стороны  , считая
, считая  известными.
известными.
30. Вычислить длину диагоналей параллелограмма, построенного на векторах 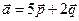 и
и  , если известно, что
, если известно, что 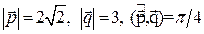 .
.
31. В прямоугольном равнобедренном треугольнике проведены медианы из вершин острых углов, вычислить угол между ними.
32. Обозначив, через  и
и  стороны ромба, выходящие из общей вершины, доказать, что диагонали ромба взаимно перпендикулярны.
стороны ромба, выходящие из общей вершины, доказать, что диагонали ромба взаимно перпендикулярны.
33. Зная, что  , определить, при каком значении коэффициента
, определить, при каком значении коэффициента  векторы
векторы  и
и  окажутся перпендикулярными.
окажутся перпендикулярными.
34. Даны разложения векторов, служащих сторонами треугольника, по двум взаимно перпендикулярным ортам:  ,
,  ,
,  . Вычислить длину медианы
. Вычислить длину медианы  треугольника
треугольника  .
.
35. Даны разложения векторов, служащих сторонами треугольника, по двум взаимно перпендикулярным ортам:  ,
,  ,
,  . Вычислить длину высоты
. Вычислить длину высоты  треугольника
треугольника  .
.
36. Зная векторы  и
и  , на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярный к стороне
, на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярный к стороне  .
.
37. Зная разложение вектора  по трем перпендикулярным ортам, вычислить длину вектора
по трем перпендикулярным ортам, вычислить длину вектора  и углы, которые он образует с каждым из ортов
и углы, которые он образует с каждым из ортов  .
.
38. Треугольник АВС задан векторами  =
=  и
и  =
=  . Выразить через векторы
. Выразить через векторы  и
и  вектор
вектор  , направленный по высоте АН.
, направленный по высоте АН.
39. Вычислить длину диагоналей параллелограмма, построенного на векторах  = 5
= 5 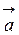 +2
+2  и
и  =
= 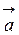 -3
-3  , если известно, что
, если известно, что  =
=  ,
,  =3 и угол между векторами
=3 и угол между векторами 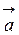 и
и  равен
равен  .
.
40. Найти угол между диагоналями параллелограмма, построенного на векторах 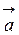 =2
=2  +
+  и
и  = -
= -  -2
-2  .
.
41. Даны два вектора: 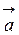 (8,4,1) и
(8,4,1) и  (2,-2,1), выходящие из одной точки. Найти вектор
(2,-2,1), выходящие из одной точки. Найти вектор  , исходящий из этой же точки, перпендикулярный вектору
, исходящий из этой же точки, перпендикулярный вектору 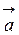 , равный ему по длине, компланарный с векторами
, равный ему по длине, компланарный с векторами 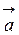 и
и  и образующий с вектором
и образующий с вектором  острый угол.
острый угол.
42. Зная две стороны треугольника  и
и  , вычислить длину его высоты
, вычислить длину его высоты  при условии, что
при условии, что  и
и  – перпендикулярные друг другу орты.
– перпендикулярные друг другу орты.
43. Разложить вектор  по взаимно перпендикулярным ортам
по взаимно перпендикулярным ортам 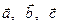 , образующим правую тройку.
, образующим правую тройку.
44. Дан вектор  , где
, где 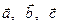 – взаимно перпендикулярные орты, образующие левую тройку. Вычислить его длину.
– взаимно перпендикулярные орты, образующие левую тройку. Вычислить его длину.
45. Вычислить объем параллелепипеда, построенного на векторах:  ,
,  ,
,  , где
, где  .
.
46. Вычислить высоту параллелепипеда, построенного на трех векторах:  ,
,  и
и  , если за основание взят параллелограмм, построенный на
, если за основание взят параллелограмм, построенный на  и
и  . Кроме того, известно, что
. Кроме того, известно, что  – взаимно перпендикулярные орты.
– взаимно перпендикулярные орты.
47. Проверить справедливость равенства  .
.
48. Найти вектор  , одновременно удовлетворяющий двум уравнениям:
, одновременно удовлетворяющий двум уравнениям:  и
и  , где
, где 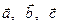 – данные векторы и
– данные векторы и  – данный скаляр.
– данный скаляр.
49. Доказать тождество ([ 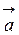 ,
,  ], [
], [  ,
,  ])=(
])=( 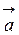 ,
,  )(
)(  ,
,  ) – (
) – ( 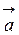 ,
,  )(
)(  ,
,  ).
).
50. Вектор  перпендикулярен векторам
перпендикулярен векторам 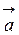 и
и  , величина угла между которыми равна
, величина угла между которыми равна  . Зная, что
. Зная, что  =3,
=3,  =6,
=6,  =3, вычислить (
=3, вычислить ( 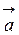 ,
,  ,
,  ).
).
51. На векторах 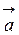 (2,3,1) и
(2,3,1) и  (-1,1,2), отложенных из одной точки, построен треугольник. Найти площадь этого треугольника, длины трёх его высот.
(-1,1,2), отложенных из одной точки, построен треугольник. Найти площадь этого треугольника, длины трёх его высот.
52. Из одной точки отложены четыре вектора 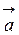 (-1,1,-1),
(-1,1,-1),  (-1,1,1),
(-1,1,1),  (5,-1,-1), и
(5,-1,-1), и  . Вектор
. Вектор  имеет длину 1 и образует с векторами
имеет длину 1 и образует с векторами 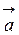 ,
,  ,
,  , равные острые углы. Вычислить координаты вектора
, равные острые углы. Вычислить координаты вектора  .
.
53. В пространстве даны две системы координат  и
и  . Начало второй системы координат имеет в первой системе координаты (1,1,2), а базисные векторы второй системы имеют в базисе первой системы координаты (4,2,1), (5,3,2) и (3,2,1) соответственно. 1) Найти координаты точки в первой системе, если известны её координаты во второй системе координат. 2) Найти координаты точки во второй системе, если известны её координаты в первой системе координат.
. Начало второй системы координат имеет в первой системе координаты (1,1,2), а базисные векторы второй системы имеют в базисе первой системы координаты (4,2,1), (5,3,2) и (3,2,1) соответственно. 1) Найти координаты точки в первой системе, если известны её координаты во второй системе координат. 2) Найти координаты точки во второй системе, если известны её координаты в первой системе координат.
54. В пространстве даны две системы координат  и
и  . Начало второй системы координат имеет в первой системе координаты (1,1,2), а базисные векторы второй системы имеют в базисе первой системы координаты (4,2,1), (5,3,2) и (3,2,1) соответственно. Найти координаты точки О во второй системе и координаты векторов
. Начало второй системы координат имеет в первой системе координаты (1,1,2), а базисные векторы второй системы имеют в базисе первой системы координаты (4,2,1), (5,3,2) и (3,2,1) соответственно. Найти координаты точки О во второй системе и координаты векторов  в базисе второй системы координат.
в базисе второй системы координат.
55. Составить уравнения прямых, проходящих через вершины треугольника А(5;-4), В(-1;3), С(-3;2) параллельно противоположным сторонам.
56. Даны вершины треугольника А(2;1), В(-1;-1), С(3;2). Составить уравнения его высот.
57. Даны вершины треугольника А(1;-1), В(-2;1) и С(3;5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану, проведённую из вершины В.
58. Даны уравнения двух сторон прямоугольника: х – 2у =0, х – 2у + 15 =0 и уравнение одной из его диагоналей 7х + у – 15 =0. Найти вершины прямоугольника.
59. Даны вершины треугольника А(2;-2), В(3;-5) и С(5;7). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине А.
60. Даны уравнения двух сторон прямоугольника 5х + 2у – 7 =0, 5х + 2у – 36 =0 и уравнение его диагонали 3х + 7у – 10 =0. Составить уравнения остальных сторон и второй диагонали этого прямоугольника.
61. Дана прямая 2х + 3у + 4=0. Составить уравнение прямой, проходящей через точку А(2,1) под углом 45 градусов к данной прямой.
62. Определить, при каком значении а прямая  1) параллельна оси абсцисс; 2) параллельна оси ординат; 3) проходит через начало координат.
1) параллельна оси абсцисс; 2) параллельна оси ординат; 3) проходит через начало координат.
63. Определить при каком значениях m и n прямая  параллельна оси ординат и пересекает ось абсцисс в точке (5,0).
параллельна оси ординат и пересекает ось абсцисс в точке (5,0).
64. Дан ромб, диагонали которого равны 4 и 10. Найти уравнения всех его сторон, зная, что оси координат направлены по его диагоналям из точки их пересечения.
65. Составить уравнение прямой, проходящей через точку С(4,-2), если эта прямая отсекает от оси ОУ отрезок вдвое больший, чем на оси ОХ.
66. Стороны АВ, ВС, и АС треугольника АВС даны соответственно уравнениями: 4х + 3у – 5 = 0, х – 3у + 10 = 0, х – 2 = 0. Определить координаты его вершин.
67. Дана прямая 2х +3у +4 = 0. Составить уравнение прямой, проходящей через точку А(2,1): 1) параллельно данной прямой, 2) перпендикулярно к данной прямой.
68. Через точку (2,-5) проходит прямая, образующая угол  с прямой
с прямой  . Составить уравнение этой прямой.
. Составить уравнение этой прямой.
69. Написать уравнение прямой, проходящей через точку (4,-6) и параллельно биссектрисе первого координатного угла.
70. Составить уравнение прямой, отсекающей на оси ОХ отрезок, равный 3, и проходящей через точку (-5,3).
71. Какой угол образует с осью ОХ прямая, проходящая через точку М(1,3) и точку пересечения медиан треугольника с вершинами А(-1,4), В(2,3), С(5,8)?
72. Из точек А(1,2) и В(3,1) проведены прямые через начало координат. Определить величину угла между этими прямыми.
73. Составить уравнение прямой, которая проходит через начало координат и образует угол 45 градусов с прямой у = 2х + 5.
74. Стороны треугольника АВС лежат на прямых: 3х – у =0 (АВ), х + 4у – 2 = 0 (ВС), 2х + 7у =0 (АС). Найти величину угла между высотой, проведенной из вершины В, и стороной АВ.
75. Даны вершины треугольника: А(4,6), В(-4,0), С(-1,-4). Составить уравнения: 1) трех его высот, 2) медианы проведенной из вершины С, 3) высоты опущенной из вершины А на сторону ВС.
76. Даны вершины двух треугольников  и
и  , а именно А(3,0), В(0,3), С(-2,-1) и
, а именно А(3,0), В(0,3), С(-2,-1) и  ,
,  ,
,  . Доказать, что стороны их соответственно параллельны, и что прямые, соединяющие сходственные вершины, пересекаются в одной точке.
. Доказать, что стороны их соответственно параллельны, и что прямые, соединяющие сходственные вершины, пересекаются в одной точке.
77. Составить уравнения сторон треугольника, зная две его вершины А(3,5) и В(6,1) и точку пересечения его медиан М(4,0).
78. Составить уравнения катетов прямоугольного треугольника, площадь которого равна 20кв.ед., если известно, что его гипотенуза лежит на оси абсцисс, а вершина прямого угла совпадает с точкой С(-1,4).
79. Через точку А(5,2) провести прямую, отсекающую равные отрезки на осях координат.
80. В равнобедренном прямоугольном треугольнике даны координаты вершины острого угла (5,7) и уравнение противолежащего катета:  . Составить уравнения двух других сторон треугольника.
. Составить уравнения двух других сторон треугольника.
81. Составить уравнения катетов прямоугольного равнобедренного треугольника, зная уравнение гипотенузы  и вершину прямого угла (4,-1).
и вершину прямого угла (4,-1).
82. Доказать, что прямая 5х – 2у – 1 =0 параллельна прямым 5х – 2у + 7 = 0, 5х – 2у – 9 = 0 и делит расстояние между ними пополам.
83. Даны три параллельные прямые: 10х + 15у –3 = 0, 2х + 3у + 5 = 0, 2х + 3у – 9 = 0. Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними.
84. Составить уравнение прямой, параллельной и равноудаленной от двух параллельных прямых х + у – 1 = 0 и х + у + 13 = 0.
85. Определить, лежит ли начало координат внутри или вне треугольника, стороны которого заданы уравнениями 7х – 5у – 11 = 0, 8х + 3у +31 = 0, х + 8у – 19 = 0.
86. Дана прямая 5х + 12у + 2 = 0. Найти уравнение прямой, параллельной данной и отстоящей от неё на расстоянии 3 единицы.
87. Составить уравнения биссектрис углов, образованных двумя прямыми:  и
и  . Проверить, что эти биссектрисы перпендикулярны друг другу.
. Проверить, что эти биссектрисы перпендикулярны друг другу.
88. Через точку М(1,2) провести прямую так, чтобы она прошла на одинаковом расстоянии от точек А(3,3) и В(5,2).
89. Даны две точки: А(2,-3) и В(5,-1). Провести прямую так, чтобы она прошла на расстоянии 6 единиц от точки А и на расстоянии 4 единицы от точки В.
90. Через начало координат и точку М(1,3) проходят две параллельные прямые. Найти их уравнения, если известно, что расстояние между этими прямыми равно  .
.
91. Сторона ромба равна 5 и высота 4,8. Через две противолежащие его вершины проходит эллипс, фокусы которого совпадают с двумя другими вершинами ромба. Составить уравнение эллипса, приняв диагонали ромба за оси координат.
92. Вершина треугольника, имеющего неподвижное основание, перемещается так, что периметр треугольника сохраняет постоянную величину. Найти траекторию вершины при условии, что основание равно 24см., а периметр равен 50см.
93. Эллипс, симметричный относительно осей прямоугольной декартовой системы координат, касается двух прямых: х + у – 5 = 0 и х – 4у – 10 = 0. Найти его уравнение.
94. Прямые  служат директрисами эллипса, малая ось которого равна 8. Найти уравнение этого эллипса.
служат директрисами эллипса, малая ось которого равна 8. Найти уравнение этого эллипса.
95. Определить эксцентриситет эллипса, зная, что 1) малая ось его видна из фокуса под прямым углом. 2) Расстояние между фокусами равно расстоянию между вершинами малой и большой осей. 3) расстояние между директрисами в четыре раза больше расстояния между фокусами.
96. На эллипсе  найти точку, отстоящую на расстоянии пяти единиц от его малой оси.
найти точку, отстоящую на расстоянии пяти единиц от его малой оси.
97. В эллипс  вписан правильный треугольник, одна из вершин которого совпадает с правой вершиной большой оси. Найти координаты двух других вершин треугольника.
вписан правильный треугольник, одна из вершин которого совпадает с правой вершиной большой оси. Найти координаты двух других вершин треугольника.
98. На эллипсе, один из фокусов которого имеет координаты (3; 0), взята точка М(4; 2,4). Найти расстояние этой точки до соответствующей директрисы, зная, что центр эллипса совпадает с началом координат.
99. Через фокус  эллипса
эллипса  проведена хорда, перпендикулярная к большой оси. Найти длину этой хорды.
проведена хорда, перпендикулярная к большой оси. Найти длину этой хорды.
100. В эллипсе  вписан прямоугольник, две противоположные стороны которого проходят через фокусы. Вычислить площадь этого прямоугольника.
вписан прямоугольник, две противоположные стороны которого проходят через фокусы. Вычислить площадь этого прямоугольника.
101. Найти уравнения сторон квадрата, описанного около эллипса  .
.
102. Через точку (2; -5) провести прямые, параллельные асимптотам гиперболы  .
.
103. На гиперболе  найти точки, касательные в которых наклонены к оси абсцисс под углом
найти точки, касательные в которых наклонены к оси абсцисс под углом  .
.
104. Дана парабола  . Провести к ней касательную образующую с прямой 4х – 2у + 9 = 0 угол
. Провести к ней касательную образующую с прямой 4х – 2у + 9 = 0 угол  .
.
105. Определить при каких значениях углового коэффициента k прямая у = kх +2 1) пересекает параболу  2) касается её.
2) касается её.
106. Определить точки пересечения эллипса  и параболы
и параболы  .
.
107. Провести касательные к гиперболе  а) через точку (-4,3), б) через точку (5, -1).
а) через точку (-4,3), б) через точку (5, -1).
108. Гипербола касается прямой  в точке М (4,2). Составить уравнение этой гиперболы.
в точке М (4,2). Составить уравнение этой гиперболы.
109. Составить уравнение гиперболы, зная уравнения ее асимптот  и уравнение одной из ее касательных
и уравнение одной из ее касательных  .
.
110. Найти общие касательные эллипса  и параболы
и параболы  .
.
111. Вычислить параметр параболы  , если известно, что она касается прямой
, если известно, что она касается прямой  .
.
112. Найти условие, при котором прямая  касается параболы
касается параболы  .
.
113. Составить уравнение общей хорды параболы  и круга
и круга  .
.
114. Через фокус параболы  проведена хорда, перпендикулярная к ее оси. Определить длину этой хорды.
проведена хорда, перпендикулярная к ее оси. Определить длину этой хорды.
115. Составить уравнения сторон треугольника, вписанного в параболу  , зная, что одна из его вершин совпадает с вершиной параболы, а точка пересечения высот совпадает с фокусом параболы.
, зная, что одна из его вершин совпадает с вершиной параболы, а точка пересечения высот совпадает с фокусом параболы.
116. Дан эллипс  . Через точку (1, 1) провести хорду, делящуюся в этой точке пополам.
. Через точку (1, 1) провести хорду, делящуюся в этой точке пополам.
117. Через точку (2, 1) провести такую хорду параболы  , которая делилась бы в данной точке пополам.
, которая делилась бы в данной точке пополам.
118. Составить уравнения плоскостей, в следующих случаях: 1) проходящей через точку  параллельно плоскости
параллельно плоскости  , 2) проходящей через точку
, 2) проходящей через точку  и ось
и ось  ,3) проходящей через две точки
,3) проходящей через две точки  и
и  параллельно оси
параллельно оси  ,
,
119. Составить уравнение плоскости, проходящей через две точки  и
и  параллельно оси
параллельно оси  .
.
120. Определить координаты точки, имеющей абсциссу, равную единице, и лежащей в плоскостях  и
и  .
.
121. Вычислить объем  пирамиды, ограниченной плоскостью
пирамиды, ограниченной плоскостью  и координатными плоскостями.
и координатными плоскостями.
122. Указать особенности расположения плоскостей по отношению к системе координат: 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  , 6)
, 6)  , 7)
, 7)  .
.
123. Написать уравнение плоскости, параллельной оси  и отсекающей на положительной полуоси
и отсекающей на положительной полуоси  отрезок длиной в три единицы, а на отрицательной полуоси
отрезок длиной в три единицы, а на отрицательной полуоси  отрезок длиной в четыре единицы.
отрезок длиной в четыре единицы.
124. Составить уравнение плоскости, отсекающей от отрицательной полуоси  отрезок, равный 5, и перпендикулярной вектору
отрезок, равный 5, и перпендикулярной вектору  .
.
125. Составить уравнение плоскости, проходящей через точку  перпендикулярно к вектору
перпендикулярно к вектору  .
.
126. Даны две точки  и
и  . Составить уравнение плоскости, проходящей через точку
. Составить уравнение плоскости, проходящей через точку  перпендикулярно к вектору
перпендикулярно к вектору  .
.
127. Плоскость  вместе с координатными плоскостями образует некоторый тетраэдр. Вычислить ребро куба, который можно поместить внутри этого тетраэдра так, что три грани его совпали с координатными плоскостями, а вершина, противолежащая началу координат, лежала на данной плоскости.
вместе с координатными плоскостями образует некоторый тетраэдр. Вычислить ребро куба, который можно поместить внутри этого тетраэдра так, что три грани его совпали с координатными плоскостями, а вершина, противолежащая началу координат, лежала на данной плоскости.
128. Вычислить расстояние между параллельными плоскостями  и
и  .
.
129. Написать уравнение плоскости, расположенной на равном расстоянии от двух данных параллельных плоскостей  и
и  .
.
130. На оси  найти точку, равноудаленную от двух плоскостей
найти точку, равноудаленную от двух плоскостей  и
и  .
.
131. Составить уравнение плоскости, проходящей через точку  и перпендикулярной двум плоскостям
и перпендикулярной двум плоскостям  и
и  .
.
132. Составить уравнение плоскости, которая проходит через точки  и
и  перпендикулярно плоскости
перпендикулярно плоскости  .
.
133. Найти точку, симметричную с началом координат относительно плоскости  .
.
134. Найти плоскость, зная, что точка  служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.
служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.
135. Через точку  проведены две плоскости: одна из них содержит ось Ох, другая – ось Оу. Вычислить угол между этими двумя плоскостями.
проведены две плоскости: одна из них содержит ось Ох, другая – ось Оу. Вычислить угол между этими двумя плоскостями.
136. Найти центр сферы, вписанной в тетраэдр, ограниченный плоскостями координат и плоскостью  .
.
137. На расстоянии трех единиц от плоскости  провести параллельную ей плоскость.
провести параллельную ей плоскость.
138. Написать уравнение плоскости, проходящей через начало координат и через две точки  и
и  .
.
139. Известны координаты вершин тетраэдра:  ,
,  ,
,  ,
,  . Составить уравнения его граней.
. Составить уравнения его граней.
140. Через линию пересечения плоскостей  и
и  провести плоскость перпендикулярную к плоскости
провести плоскость перпендикулярную к плоскости  .
.
141. В пучке, определяемом плоскостями  и
и  , найти плоскости, перпендикулярные к этим основным плоскостям.
, найти плоскости, перпендикулярные к этим основным плоскостям.
142. Написать уравнение плоскости, перпендикулярной к плоскости  и пересекающей ее по прямой, лежащей в плоскости (ху).
и пересекающей ее по прямой, лежащей в плоскости (ху).
143. Написать уравнения плоскостей, делящих пополам двугранные углы между плоскостями  и
и  .
.
144. На оси  найти точку, равноудаленную от двух плоскостей:
найти точку, равноудаленную от двух плоскостей:  и
и  .
.
145. Определить угол между двумя прямыми  и
и  .
.
146. Через точку (2,-5,3) провести прямую параллельную прямой  .
.
147. Написать уравнение перпендикуляра, опущенного из точки А(2,3,1) на прямую  .
.
148. Из всех прямых, пересекающих две прямые:  и
и  , найти ту, которая была бы параллельна прямой
, найти ту, которая была бы параллельна прямой  .
.
149. Даны точки пересечения прямой с двумя координатными плоскостями  и
и  . Вычислить координаты точки пересечения этой же прямой с третьей координатной плоскостью.
. Вычислить координаты точки пересечения этой же прямой с третьей координатной плоскостью.
150. Составить уравнения прямой, которая проходит через точку А(1,-5,3) и образует с осями координат углы, соответственно равные  .
.
151. Составить уравнения прямой, проходящей через точки пересечения плоскости  с прямыми
с прямыми  и
и  .
.
152. Из точки (3,-2,4) опустить перпендикуляр на плоскость  .
.
153. Написать уравнение плоскости, которая проходит через точку (3,1,-2) и через прямую  .
.
154. Через прямую  провести плоскость, перпендикулярную к плоскости
провести плоскость, перпендикулярную к плоскости  .
.
155. Провести плоскость через перпендикуляры, опущенные из точки (-3,2,5) на плоскости  и
и  .
.
156. Написать уравнение плоскости, проходящей через прямую  и параллельной прямой
и параллельной прямой  .
.
157. Через прямую  провести плоскость, параллельную плоскости
провести плоскость, параллельную плоскости  .
.
158. Через точку Р(1,0,7) параллельно плоскости  провести прямую так, чтобы она пересекала прямую
провести прямую так, чтобы она пересекала прямую  .
.
159. На прямой  найти точку, ближайшую к точке (3,2,6).
найти точку, ближайшую к точке (3,2,6).
160. Найти центр кривой  .
.
161. Найти преобразованное уравнение кривой  , если начало координат будет перенесено в точку (-3,-1).
, если начало координат будет перенесено в точку (-3,-1).
162. Найти центр кривой  .
.