Общее уравнение кривых второго порядка
Общее уравнение кривой второго порядка на плоскости имеет вид
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0, (39)
где A2 + B2 + C2 
0, (A, B, C, D, E, F) 
R. Оно определяет все возможные конические сечения произвольным образом расположенные на плоскости. Из коэффициентов уравнения (39) составим два определителя
, 
, (40)
– называется дискриминантом уравнения (39), а 
– дискриминантом старших членов уравнения. При 0 уравнение (39) определяет: > 0 – эллипс; < 0 – гиперболу; = 0 – параболу. В случае = 0 кривые вырождаются в точку или прямые линии.
От общего уравнения (39) можно перейти к каноническому уравнению, если исключить линейные и перекрестный члены путем перехода в новую систему координат, совпадающую с осями симметрии фигуры. Заменим в (39) x на x* + a и y на y* + b, где a, b некоторые константы. Выпишем полученные коэффициенты при х* и y* и приравняем их к 0
(Aa + Bb + D)x* = 0, (Cb + Ba + E)y* = 0. (41)
В результате уравнение (39) примет вид
A(x*)2 + 2B(x*)(y*) + C(y*)2 + F* = 0, (42)
где коэффициенты А, B, C не изменились, а F* = 
/ . Решение системы уравнений (41) определит координаты центра симметрии фигуры
, 
. (43)
Если B = 0, то a = –D/A, b = –E/C и исключать линейные члены в (39) удобно методом приведения к полному квадрату:
Ax2 + 2Dx = A(x2 + 2xD/A + (D/A)2 – (D/A)2) = A(x + D/A)2 – D2/A.
В уравнении (42) совершим поворот координат на угол a (38). Выпишем полученный коэффициент при перекрестном члене x*y* и приравняем его к 0
[sin2 
(A–C) + 2cos2 B]x*y* = 0. (44)
Условие (44) определяет необходимый угол поворота осей координат до их совпадения с осями симметрии фигуры и принимает вид
tg2 = 
. (45)
Уравнение (42) принимает форму
A+X2 + C+Y2 + F* = 0 (46)
от которой легко перейти к каноническому уравнению кривой
. (47)
Коэффициенты A+, C+, при условии (45), можно представить как корни вспомогательного квадратного уравнения
t2 – (A + C)t + = 0. (48)
В результате определены положение и направление осей симметрии фигуры, ее полуоси
a2 = 
, b2 = 
и она может быть построена геометрически.
В случае = 0 имеем параболу. Если её ось симметрии параллельна оси Ох, то уравнение сводится к виду
, (49)
если нет, то к виду
, (50)
где выражения в скобках, приравненные к 0, определяют линии новых осей координат: 
, 
.
Решение типичных задач
Пример 15. Привести уравнение 2x2 + 3y2 – 4x + 6y – 7 = 0 к каноническому виду и построить кривую.
Решение. B = 0, 
= –72 0, 
= 6 > 0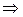 
эллипс.
Выполним приведение к полному квадрату:
2(x – 1)2 + 3(y + 1)2 – 12 = 0.
Координаты центра симметрии (1; –1), линейное преобразование X = x – 1, Y = y + 1 приводит уравнение к каноническому виду 
.
Пример 16. Привести уравнение 2xy = a2 к каноническому виду и построить кривую.
Решение. B = 1, 
= a2 0, 
= –1 < 0 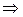гипербола.
Центр системы координат находится в центре симметрии кривой, т.к. в уравнении нет линейных членов. Совершим поворот осей на угол a. По формуле (45) имеем tg2a = B/(A – C) = 
, т.е. a = 45°. Коэффициенты канонического уравнения (46) A+, C+ определяются уравнением (48): t2 = 1 или t1,2 = 
1 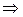A+ = 1, C+ = –1, т.е.
X2 – Y2 = a2 или 
. Таким образом, уравнение 2ху = а2 описывает гиперболу с центром симметрии в (0; 0). Оси симметрии располагаются по биссектрисам координатных углов, асимптотами служат оси координат, полуоси гиперболы равны а.
Пример 17. Привести уравнение x2 + 6х + y + 10 = 0 к каноническому виду и построить кривую.
Решение. B = 0, 
= –¼ 0, 
= 0 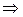парабола.
Выполним приведение к полному квадрату:
(x + 3)2 = –(y + 1).
Координаты центра симметрии (–3; –1), линейное преобразование
X = x + 3, Y = y + 1 приводит уравнение к каноническому виду X2 = –Y, где фокальный параметр р = 1/2.
Задачи для самостоятельного решения
Привести к каноническому виду следующие уравнения и построить соответствующие кривые:
21) 4x2 + 9y2 – 16x – 18y – 11 = 0; 22) x2 + 2х – y = 0;
23) x2 – 9y2 + 6x + 18y – 9 =0; 24) 9x2 + y2 – 18x + 2y+1 = 0;
25) 2x2 + 4х + y – 2 = 0; 26) 3x2 – 6х – y + 2 = 0;
27) x2 + 4y2 – 8x – 9y +16 = 0; 28) 4x2 + 8х – y – 5 = 0;
29) 9x2 – y2 + 18x + 2y – 1 = 0; 30) 9x2 – 4y2 +36x + 16y – 16 = 0.