Доказательство.
1) Пусть векторы  ,
,  ,
, 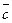 Î V3 – компланарны, и пусть
Î V3 – компланарны, и пусть  =
=  ,
,  =
=  ,
,  =
= 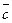 и точки O,A,B,C лежат в одной плоскости (то есть O Î (ABC)).
и точки O,A,B,C лежат в одной плоскости (то есть O Î (ABC)).
Тогда векторы  ,
,  ,
, 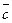 можно рассматривать как элементы V2, построенные на множестве направленных отрезков плоскости (АВС).
можно рассматривать как элементы V2, построенные на множестве направленных отрезков плоскости (АВС).
1 случай. Если векторы  и
и  коллинеарны, то существуют два числа a, b Î R такие, что хотя бы одно из этих чисел отлично от нуля (a2 + b2 ≠ 0 ) и a
коллинеарны, то существуют два числа a, b Î R такие, что хотя бы одно из этих чисел отлично от нуля (a2 + b2 ≠ 0 ) и a  + b
+ b  = q. Возьмем g = 0, тогда среди чисел a, b, g все равно есть число отличное от нуля a
= q. Возьмем g = 0, тогда среди чисел a, b, g все равно есть число отличное от нуля a  + b
+ b  + g
+ g 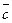 = (a
= (a  +b
+b  ) + 0
) + 0 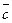 = q + q = q.
= q + q = q.

2 случай. Если векторы  и
и  не коллинеарны, то они образуют базис пространства V2 , и существуют два числа a, b Î R такие
не коллинеарны, то они образуют базис пространства V2 , и существуют два числа a, b Î R такие 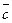 = a
= a  + b
+ b  . Возьмем g = -1, тогда среди чисел a, b, g есть число отличное от нуля (g = -1) и a
. Возьмем g = -1, тогда среди чисел a, b, g есть число отличное от нуля (g = -1) и a  + b
+ b  + g
+ g 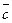 = (a
= (a  +b
+b  ) + (-1)
) + (-1) 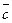 =
= 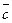 -
- 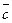 = q.
= q.

РИС. 24 (1, 2)
2) Пусть существуют три числа a, b, g Î R такие, что хотя бы одно из этих чисел отлично от нуля (a2 + b2 + g2 ≠ 0 ) и a  + b
+ b  + g
+ g 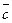 = q.
= q.
Без ограничения общности пусть g ≠ 0. Тогда вектор 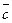 можно выразить через векторы
можно выразить через векторы  и
и  :
: 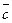 = -
= - 
 -
- 
 .
.
Отложим векторы  ,
,  ,
, 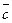 от одной точки O:
от одной точки O:  =
=  ,
,  =
=  ,
,  =
= 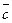 . Покажем, что точки O,A,B и C лежат в одной плоскости.
. Покажем, что точки O,A,B и C лежат в одной плоскости.
1 случай. Если векторы  и
и  коллинеарны, то вектор
коллинеарны, то вектор 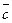 так же коллинеарен векторам
так же коллинеарен векторам  и
и  (см. необходимое и достаточное условие коллинеарности векторов). Следовательно, точки O,A,B,C лежат на одной прямой, то есть существует плоскость, которая проходит через все эти точки.
(см. необходимое и достаточное условие коллинеарности векторов). Следовательно, точки O,A,B,C лежат на одной прямой, то есть существует плоскость, которая проходит через все эти точки.
2 случай. Векторы  и
и  не коллинеарны. Рассмотрим плоскость (OAB) и векторное пространство V2, построенное по направленным отрезкам данной плоскости. Построим направленный отрезок
не коллинеарны. Рассмотрим плоскость (OAB) и векторное пространство V2, построенное по направленным отрезкам данной плоскости. Построим направленный отрезок  =-
=- 
 -
- 
 (по правилу параллелограмма для суммы двух векторов). Тогда точки O,A,B,C лежат в одной плоскости и
(по правилу параллелограмма для суммы двух векторов). Тогда точки O,A,B,C лежат в одной плоскости и  =
= 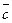 , следовательно, векторы
, следовательно, векторы  ,
,  ,
, 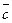 компланарны (по определению).
компланарны (по определению).