Общие сведения

Определение 1.

Многоугольник называется вписанным Б окруж - ность, если все его вершины принадлежат этой окружности.

Окружность при этом называется описанной около многоугольника.

Теорема 1.

Около всякого треугольника можно описать единственную окружность. Ее центром является точка пересечения серединных перпендикуляров к сторонам треугольника.

Теорема 2.

Отношение стороны треугольника к синусу противо - лежащего угла равно диаметру описанной окружности.

Теорема 3.

Радиус R окружности, описанной около треугольника, выражается формулой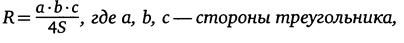

Определение 2.

Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Окру ность при этом называется вписанной в многоугольник

Теорема 4.

В любой треугольник можно вписать единственную окружность. Ее центром является точка пересечения биссектрис треугольника.

Теорема 5.

Радиус r окружности, вписанной в треугольник, выражается формулой.

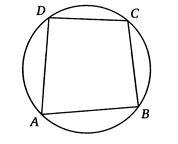
Теорема 6.

Суммы противоположных углов четырехугольника, вписанного в окружность, равны 180°

Теорема 7.

суммы противоположных сторон четырехугольника, описанного около окружности, равны