Силы Ампера и Лоренца. Действие магнитного поля на проводники с током

 

1. Появление силы , действующей на проводник с током в магнитном поле, было изучено французским физиком Ампером. Поэтому она называется силой Ампера. Ампер обнаружил, что сила, действующая на проводник с током, зависит от силы тока, длины проводника в магнитном поле.

Рис.4.7

Выберем прямолинейный участок (рис.4.7); согласно закону Ампера: . В системе СИ k = 1, получаем: (4.13) - это закон Ампера в векторной форме.

Закон Ампера: сила, действующая на проводник с током в магнитном поле, равна произведению силы тока на векторное произведение .

Проводник прямолинейный, магнитное поле однородно, т.е. , a = const:

(4.14)

Направление вектора силы определяется по правилу векторного произведения; если перпендикулярен 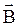, то удобно использовать правило левой руки (рис.4.8):

Рис.4.8. Правило левой руки

если расположить левую руку таким образом, чтобы линии индукции внешнего магнитного поля входили в ладонь, пальцы указывали направление тока, то большой палец укажет направление вектора силы. Таким образом, магнитная индукция – величина, численно равная силе, с которой действует магнитное поле на единицу длины прямолинейного проводника, располо-женного перпендикулярно к направлению поля, если по проводнику протекает ток силой 1 А.

2. Рассмотрим случай взаимодействия двух бесконечных параллельных проводников, по которым текут токи I₁ и I₂ (рис.4.9). В зоне расположения проводника 1 действует магнитное поле , созданное проводником 2. На участок проводника ₁ действует сила, направление которой легко найти по правилу левой руки. Магнитное поле с индукцией для проводника 1 является внешним.

Рис.4.9

Аналогично рассуждая, можно найти силу , действующую на участок проводника 2 - 2. Из рисунка видно, что параллельные проводники с одинаковым направлением тока притягиваются. Найдем значение силы . По закону Ампера значение силы по модулю равно: (4.15) где a- угол между векторами 1 и . В случае параллельных токов sina=1, тогда (4.16)

В соответствии с уравнением для индукции прямого тока

(4.17)

получаем:

(4.18)

Найдем силу, действующую на единицу проводника:

или

(4.19)

Выражение (4.19) – закон Ампера.

3. Сила, действующая в магнитном поле на проводник с током, – результат действия поля на движущиеся электрические заряды. Если просуммировать силы, действующие на все электрические заряды, то получим силу действия на проводник в целом, т.е. силу Ампера.

Силу, действующую на движущийся в магнитном поле единичный заряд, называют силой Лоренца.

Сила Ампера

(4.20)

(4.21)

где n – объемная плотность зарядов; q – величина одного заряда; u – скорость упорядоченного движения зарядов; S – площадь поперечного сечения проводника.

Подставим в (4.20) формулу (4.21):

(4.22)

Вместо в векторное произведение ввели , т.к. и сонаправлены.

- рассматриваемый объем; - число зарядов в рассматриваемом объеме.

Чтобы найти силу, действующую на один заряд, нужно разделить dFна число зарядов:

(4.23)

 

Рис.4.10. Направление вектора силы Лоренца

 

Направление силы Лоренца, так же как и силы Ампера, определяется по правилу левой руки (см.рис.4.8 и 4.10).

4. Если проводник в целом движется со скоростью v, то эта скорость на величине силы Ампера не скажется. Дело в том, что в проводнике количество положительных и отрицательных зарядов одинаково, а силы, действующие на положительные заряды, противоположны силам, действующим на отрицательные заряды.

Сила Лоренца перпендикулярна направлению движения заряда, поэтому работа данной силы равна нулю и ее действие не сопровождается изменением энергии заряда.

Постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей, и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Под действием магнитного поля заряд изменяет направление движения. Как известно из механики, сила, перпендикулярная скорости, обуславливает центростремительное ускорение:

(4.24)

где R – радиус кривизны траектории частицы.

Если частица движется с постоянной скоростью, то радиус не изменяется. В случае движения заряженной частицы силой, действующей перпендикулярно скорости, является сила Лоренца. Следовательно, ускорение можно найти:

(4.25)

где m – масса частицы.

Если вектор скорости частицы , влетающей в магнитное поле, перпендикулярен 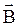, то в соответствии с уравнением (4.23) получаем:

(sina=1). (4.26)

Тогда

(4.27)

С учетом (4.24)

Получаем

(4.28)

Если скорость и индукция постоянны, то R тоже величина неизменная, т.е. частица будет вращаться по окружности радиуса R.

Если частица влетает в магнитное поле под углом к вектору магнитной индукции (рис.4.11), то вектор скорости можно разложить на две составляющие:

Рис.4.11

u1=u×sina - составляющая, перпендикулярная вект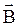ору ; u2=u×cosa - составляющая, параллельная вектору .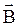

Составляющая u₁ обуславливает вращение частицы по окружности радиуса R: ,

а составляющая u₂ – движение вдоль вектора 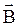, т.е. частица будет двигаться по спирали (рис.4.12).

 

Рис.4.12

 

Пройдя расстояние 2pR по окружности, в горизонтальном направлении частица пройдет расстояние l, т.е. переместится из точки А в точку В.

Время движения частицы из точки А в точку В равно периоду ее обращения по спирали:

(4.29)

Шаг спирали

l=u₂T=u×cosa×T.(4.30)