Коэффициенты тяготения f.

Если имеет место равное взаимное тяготение между абонентами всей сети, то естественно, что нагрузка 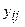пропорциональна доле входящей нагрузки j-и станции относительно суммарной нагрузки всей сети, т. е.

(2.13)

.Так как

,

Если соотношения (2.13) выполняются на сети для любых значений i и j, то, как уже отмечено, тяготение между станциями будет равномерным. Однако, как правило, тяготение между станциями является неравномерным и

.

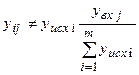Отношение между левой и правой частью этого неравенства принято называть коэффициентом тяготения или, точнее, коэффициентом тяготения f_ij абонентов станции i к абонентам станции j:

. (2.14)

Коэффициент тяготения f_ij , показывает, во сколько раз фактический поток от станции i к станции j (у_ij) больше или меньше того потока, который был бы между этими станциями, если бы имело место равномерное тяготение. При равномерном тяготении выполняются соотношения (2.13) и f_ij =1 ( j, i=1,2,…,m ).

В отличие от коэффициентов тяготения f_ij, .коэффициенты распределения .нагрузки k_ij определяют пропорцию распределения исходящей нагрузки и между всеми станциями сети. Пусть для телефонной сети заданы для всех станций значения исходящих нагрузок (i==l, 2, …, m) и все коэффициенты f_ij сведенные в матрицу (2.15)

(2.15)

Из (2.14) следует, что

Отсюда

(i=1,2,…,m) (2.16)

так как 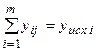.Соотношения (2.16) «представляют собой систему из m уравнений с m неизвестными y_{вx j} которая имеет единственное решение, если определитель матрицы . Определив из этих соотношений значения y_{вx j} (j=l, 2, ..., m), вычисляют все межстанционные потоки 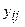по формуле (2.17), полученной из (2.14):

(2.17)

Из вычисленных значений у_ij, составляется требуемая матрица (2.4).