Пример 2.3

Имеется три тела с одинаковыми внешними размерами, но с разными массами х₁, х₂ и х₃. Необходимо определить энтропию, связанную с нахождением наиболее тяжелого из них, если сравнивать веса тел можно только попарно.

Последовательность действий достаточно очевидна: сравниваем вес двух любых тел, определяем из них более тяжелое, затем с ним сравниваем вес третьего тела и выбираем наибольший из них. Поскольку внешне тела неразличимы, выбор номеров тел при взвешивании будет случаен, однако общий результат от этого выбора не зависит. Пусть опыт ее состоит в сравнении веса двух тел, например, 1-го и 2-го. Этот опыт, очевидно, может иметь два исхода: А₁ – х₁ > х₂; его вероятность р(А₁) = 1/2; исход А₂ - x₁ < х₂; также его вероятность р(А₂) = 1/2.

Опыт β - сравнение весов тела, выбранного в опыте α, и 3-го - имеет четыре исхода: B₁, - х₁ > х₃, B₂ – х₁ < х₃, B₃ - х₂ > х₃, В₄ - х₂ < х₃; вероятности исходов зависят от реализовавшегося исхода α - для удобства представим их в виде таблицы:

Вновь, воспользовавшись формулами (2.8) и (2.9) и с учетом свойства (1) п.2.1.2, находим:

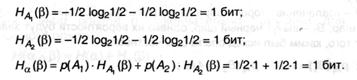
Следовательно, энтропия сложного опыта, т.е. всей процедуры испытаний:

 

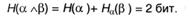
Универсальной формой представления информации является дискретная форма, т.е. представление информации с помощью некоторого набора знаков. В частности, именно таким образом представленная информация обрабатывается компьютером, передается по компьютерным и некоторым иным линиям связи. Сообщение есть последовательность знаков алфавита.

Для оценки информации, связанной с выбором одного знака алфавита с учетом неравной вероятности их появления в сообщении (текстах) можно опять воспользоваться формулой Шеннона, которая утверждает, что если р_i - вероятность (относительная частота) знака номер i данного алфавита из N знаков, то среднее количество информации, приходящейся на один знак есть

 

Представленные ниже задачи являются контрольным заданием. Решения необходимо оформить в виде текстового документа и предоставить на проверку преподавателю.