Свойства алгебраических операций.

Определение. Алгебраическая операция *, определенная на множествеА называется коммутативной, если она подчиняется закону коммутативности, т.е. для любых двух элементов х и у множества А выполняется равенство: х*у = у*х.

В школьных учебниках математики, когда говорят об операцияхсложения и умножения чисел, это свойство называется переместительным законом.

Определение. Алгебраическая операция *, определенная на множествеА называется ассоциативной, если она подчиняется закону ассоциативности, т.е. для любых трех элементов х, у, z множества А выполняется равенство: .

Здесь сначала определяется результат операции в скобках, а затем еще раз применяется операция к оставшимся двум элементам. При этом, если результат операции не зависит от способа расстановки скобок, то операция называется ассоциативной. В школьных учебниках математики, когда говорят об операциях сложения и умножения чисел, это свойство называется сочетательным законом.

Пусть на множестве А определены две алгебраических операции, которые мы обозначим символами * и .

Определение. Говорят, что операция * дистрибутивна относительно операции , если верны два равенства:

и .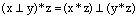

В школьных учебниках математики, когда говорят об операцияхсложения и умножения чисел, это свойство называют распределительным законом умножения относительно сложения.

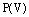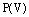Пример. Пусть дано некоторое множество . Обозначим через – множество всех подмножеств множества . Тогда на множестве определены две операции: объединение и пересечение множеств. Действительно, для любых двух подмножеств А и В множества , и – тоже подмножества множества . Легко проверяется (например, с помощью диаграмм Венна), что обе операции являются коммутативными, ассоциативными и каждая из них является дистрибутивной относительно другой.