Свойства основной задачи линейного программирования
При решении задач линейного программирования используются некоторые общие свойства, которые можно проиллюстрировать на примере задач с двумя свободными переменными.
1) Решение основной задачи линейного программирования, если только оно существует, не может лежать внутри области допустимых решений, а только на ее границах.
2) Решение основной задачи линейного программирования может быть не единственным, если прямая, определяющая целевую функцию, параллельна той стороне области допустимых решений, где функционал достигает максимума. В этом случае задача имеет бесконечное множество оптимальных решений, как показано на рис. 4.4.
|
 |
3) Основная задача линейного программирования может не иметь решений даже в случае существования области допустимых решений, если область не ограничена в направлении оптимальности (рис. 4.5).
|
 |
4) Решение основной задачи линейного программирования, максимизирующее или минимизирующее целевую функцию, всегда достигается в одной из вершин области допустимых решений. Решение, лежащее в одной из вершин области допустимых решений, называется опорным или базисным решением.
5) Чтобы найти оптимальное решение, достаточно перебрать все вершины или опорные точки области допустимых решений и выбрать из них ту, где функционал достигает экстремума.
6) Если число свободных переменных основной задачи линейного программирования при n базисных равно двум и решение основной задачи существует, то оно всегда достигается в точке, где, по крайней мере, две из переменных обращаются в нуль. Например, x4 = 0, x3 = 0 в точке К (рис. 4.6).
|
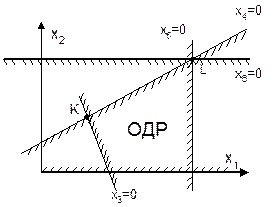 |
Случай, когда в оптимальном решении обращается в нуль не две, а более переменных, называется вырожденным (точка L на рис 4.6).