Итерационная формула.
Итерация градиентного метода с дроблением шага для задачи (1), (2) имеет вид
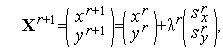
| (3) |
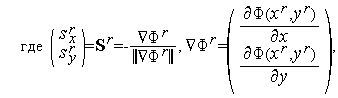
| (4) |
а величина шага  находится из условия
находится из условия
| (5) |
Найдем явные выражения для частных производных функции  (
( 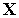 ):
):
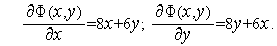
| (6) |
Таким образом, из (3), (4), (6) имеем искомую итерационную формулу градиентного метода с дроблением шага для задачи (1), (2).
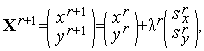
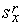 =-
=-  ,
, 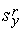 =-
=- 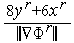 ,
,

| (7) |
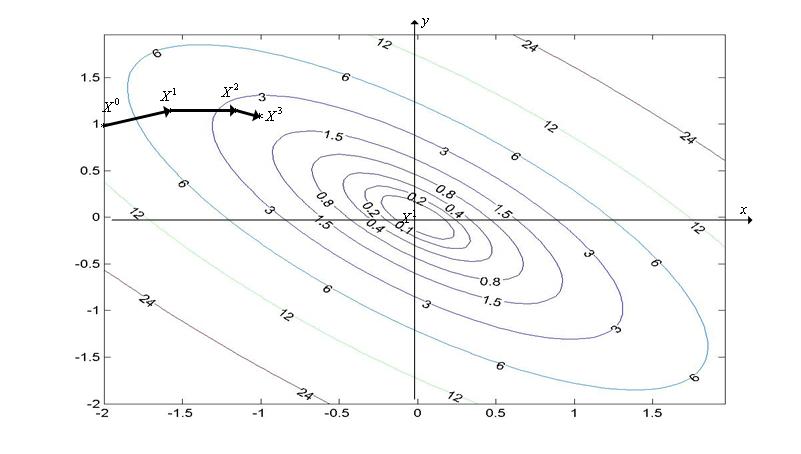
Первая итерация (  =0).
=0).
Из формул (6), (7) последовательно имеем
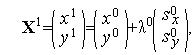

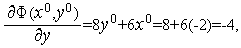
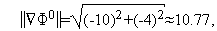
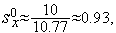
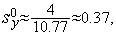
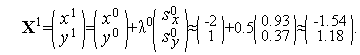
Таким образом, 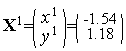 (см. рис. 1).
(см. рис. 1).
Условие (5) на первой итерации имеет вид
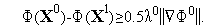
Поскольку
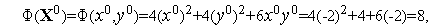
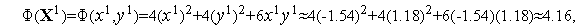
левая часть этого неравенства равна  . Его правая часть, легко видеть, равна
. Его правая часть, легко видеть, равна 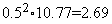 .
.
Таким образом, на первой итерации условие (5) выполняется и величина шага 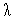 должна быть изменена:
должна быть изменена: 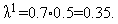
Вторая итерация (  =1).
=1).
Аналогично первой итерации последовательно имеем
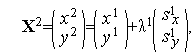
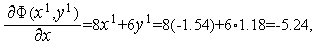
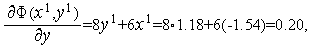
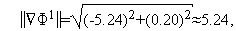
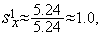
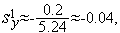
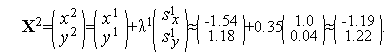
Таким образом, 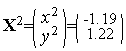 (см. рис. 1).
(см. рис. 1).
Условие (5) на второй итерации имеет вид

Поскольку

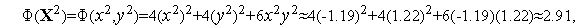
левая часть этого неравенства равна 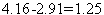 . Его правая часть, легко видеть, равна
. Его правая часть, легко видеть, равна  .
.
Таким образом, на второй итерации условие (5) выполняется и величина шага 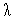 должна быть изменена:
должна быть изменена: 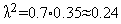 .
.
Третья итерация (  =2).
=2).
Аналогично первой итерации последовательно имеем
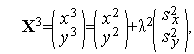
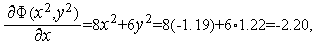
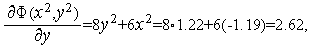
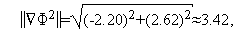

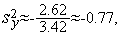
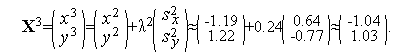
Таким образом, 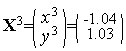 (см. рис. 1).
(см. рис. 1).
Условие (5) на третьей итерации имеет вид
 (
( 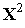 )-
)-  (
( 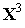 )
) 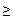 0.5
0.5 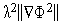 .
.
Поскольку
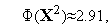
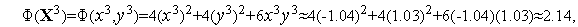
левая часть этого неравенства равна 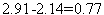 . Его правая часть, легко видеть, равна
. Его правая часть, легко видеть, равна 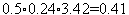 .
.
Таким образом, на третьей итерации условие (5) выполняется и величина шага 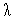 должна быть изменена:
должна быть изменена: 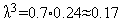 .
.
|
Рис. 1. Фрагмент (три итерации) траектории поиска минимума функции (2) градиентным методом с дроблением шага, исходя из точки X0=(x0,y0)=(-2.0,1.0).
7.2 Метод оптимизации Ньютона
Положим, что функция  (
(  ) всюду дважды дифференцируема в
) всюду дважды дифференцируема в 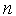 -мерном евклидовом пространстве
-мерном евклидовом пространстве  .
.
Рассмотрим следующую многомерную задачу локальной безусловной оптимизации: найти минимум критерия оптимальности  (
(  ), определенного в
), определенного в 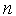 -мерном евклидовом пространстве
-мерном евклидовом пространстве  ,
,
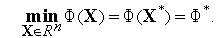
| (1) |
Обоснование метода оптимизации Ньютона.
Рассмотрим первые три члена разложения функции  (
(  ) в ряд Тейлора в окрестности точки
) в ряд Тейлора в окрестности точки  :
:
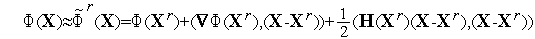
| (2) |
Здесь  (
(  ) - матрица Гессе функции
) - матрица Гессе функции  (
(  ). Из (2) следует, что градиент функции
). Из (2) следует, что градиент функции 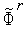 (
(  ) равен
) равен
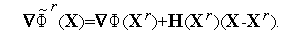
| (3) |
Если матрица Гессе  (
(  ) положительно определена, то функция
) положительно определена, то функция 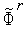 (
(  ) достигает минимума в точке, в которой градиент этой функции равен нулевому вектору.
) достигает минимума в точке, в которой градиент этой функции равен нулевому вектору.
Таким образом, в точке  минимума функции
минимума функции 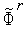 (
(  ) справедливо равенство
) справедливо равенство
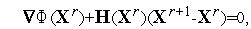
| (4) |
где 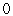 -
-  -мерный вектор нулей. Отсюда получаем итерационную формулу
-мерный вектор нулей. Отсюда получаем итерационную формулу
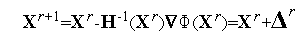
| (5) |
для отыскания очередного приближения к точке минимума функции  (
(  ). Здесь
). Здесь
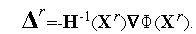
| (6) |
Выражение (5) представляет собой итерационную формулу решения системы уравнений (4) широко известным методом касательных (методом Ньютона) – см. параграф 4.8. Этим фактом объясняется название рассматриваемого метода оптимизации.
Найдем скалярное произведение градиента функции  (
(  ) в точке
) в точке  и вектора
и вектора 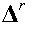 :
:
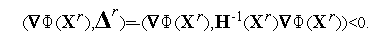
| (7) |
Последнее неравенство справедливо в силу постулируемой положительной определенности матрицы Гессе в точке  . Геометрически неравенство (7) означает, что вектор
. Геометрически неравенство (7) означает, что вектор 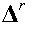 образует тупой угол с градиентом целевой функции
образует тупой угол с градиентом целевой функции  (
(  ) в точке
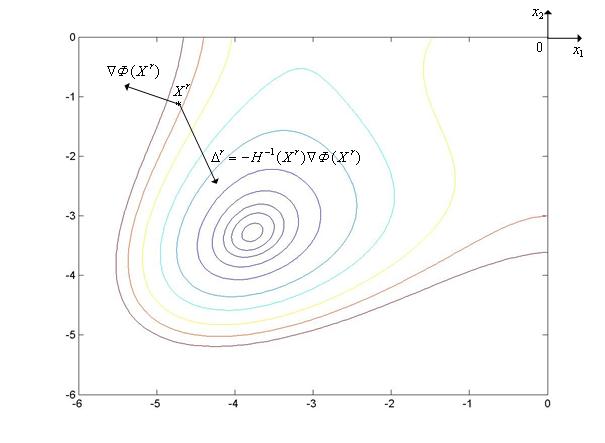
) в точке  (см. рис. 1). Таким образом, при минимизации овражных функций вектор
(см. рис. 1). Таким образом, при минимизации овражных функций вектор 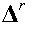 может составлять с осью оврага меньший угол, чем вектор антиградиента. Эта особенность делает метод оптимизации Ньютона, вообще говоря, более эффективным, чем градиентный метод наискорейшего спуска.
может составлять с осью оврага меньший угол, чем вектор антиградиента. Эта особенность делает метод оптимизации Ньютона, вообще говоря, более эффективным, чем градиентный метод наискорейшего спуска.
|
Рис. 1. К обоснованию метода многомерной оптимизации Ньютона.
Отметим трудности, которые могут возникать при использовании итерационной формулы (5):
- Если размерность пространства
 велика, то обращение на каждой итерации матрицы Гессе
велика, то обращение на каждой итерации матрицы Гессе  (
(  ) может потребовать значительных вычислительных ресурсов;
) может потребовать значительных вычислительных ресурсов; - Значение минимизируемой функции
 (
(  ) в точке
) в точке 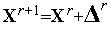 может превышать значение функции в предыдущей точке
может превышать значение функции в предыдущей точке  вследствие того, что направление
вследствие того, что направление  ведет к уменьшению
ведет к уменьшению  (
(  ), но величина шага слишком велика;
), но величина шага слишком велика; - Направление спуска, определяемое вектором
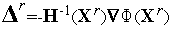 , ведет к убыванию целевой функции только при положительной определенности матрицы Гессе
, ведет к убыванию целевой функции только при положительной определенности матрицы Гессе  (
(  ). Это приводит к тому, что на каждой итерации необходимы вычислительные затраты на проверку обусловленности этой матрицы. Указанная матрица может быть плохо обусловленной. Более того, указанная матрица может быть вырожденной и, поэтому, не иметь обратной матрицы.
). Это приводит к тому, что на каждой итерации необходимы вычислительные затраты на проверку обусловленности этой матрицы. Указанная матрица может быть плохо обусловленной. Более того, указанная матрица может быть вырожденной и, поэтому, не иметь обратной матрицы.
Вследствие этих трудностей итерационная формула (5) в «чистом» виде не используется в вычислительной практике.
Для того чтобы избежать обращения матрицы Гессе, на практике вектор 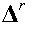 находят обычно из следующей системы линейных алгебраических уравнений (СЛАУ), вытекающей из равенства (6):
находят обычно из следующей системы линейных алгебраических уравнений (СЛАУ), вытекающей из равенства (6):
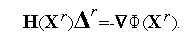
| (8) |
СЛАУ (8) может быть решена различными численными методами (например, прямыми методами, итерационными методами).
Величина шага в направлении 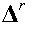 , которая приводит к убыванию функции
, которая приводит к убыванию функции  (
(  ), может быть обеспечена путем добавления в итерационную формулу (5) коэффициента
), может быть обеспечена путем добавления в итерационную формулу (5) коэффициента 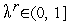 , т.е. путем использования вместо формулы (5) итерационной формулы
, т.е. путем использования вместо формулы (5) итерационной формулы
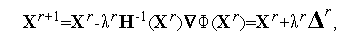
| (9) |
где коэффициент 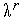 выбирают тем или иным способом так, чтобы обеспечить условие
выбирают тем или иным способом так, чтобы обеспечить условие 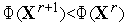 .
.
Для того, чтобы направление спуска независимо от определенности матрицы Гессе  (
(  ) вело у убыванию функции
) вело у убыванию функции  (
(  ), в качестве вектора
), в качестве вектора 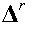 можно использовать вектор
можно использовать вектор
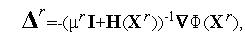
| (10) |
где 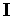 -
-  -единичная матрица, а
-единичная матрица, а  - параметр, выбираемый так, чтобы матрица
- параметр, выбираемый так, чтобы матрица 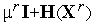 являлась положительно определенной.
являлась положительно определенной.
Схема метода оптимизации Ньютона.
Рассмотрим схему одной из модификаций метода оптимизации Ньютона, в которой используется итерационная формула (9) и вектор 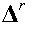 находят путем решения на каждой итерации СЛАУ (8).
находят путем решения на каждой итерации СЛАУ (8).
1. Задаем начальную точку  , начальную величину шага
, начальную величину шага 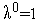 и коэффициент дробления шага
и коэффициент дробления шага 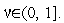 Полагаем счетчик числа итераций
Полагаем счетчик числа итераций 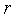 =0.
=0.
2. Вычисляем в точке  вектор градиента
вектор градиента 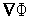 (
(  ) и матрицу Гессе
) и матрицу Гессе  (
(  ).
).
3. Решаем СЛАУ (8) и находим вектор 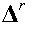 .
.
4. По формуле (9) вычисляем компоненты вектора  .
.
5. Вычисляем величину 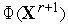 - значение функции
- значение функции  (
(  ) в точке
) в точке  .
.
6. Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то полагаем 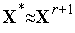 , и завершаем итерации. Иначе – переходим к следующему пункту.
, и завершаем итерации. Иначе – переходим к следующему пункту.
7. Если 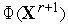 <
< 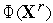 , то полагаем
, то полагаем 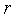 =
= 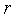 +1 и переходим к п.2. Иначе – фиксированное число раз полагаем
+1 и переходим к п.2. Иначе – фиксированное число раз полагаем 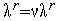 и переходим к пункту 4
и переходим к пункту 4 
В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций:
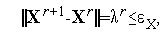
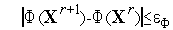
или условие
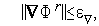
где 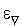 - константа, определяющая требуемую точность решения по градиенту функции
- константа, определяющая требуемую точность решения по градиенту функции  (
(  ).
).
Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
8.1 Метод с возвратом при неудачном шаге. Метод наилучшей пробы
Рассматривается следующая многомерная задача локальной безусловной оптимизации: найти минимум критерия оптимальности  (
(  ), определенного в
), определенного в 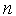 -мерном евклидовом пространстве
-мерном евклидовом пространстве  ,
,
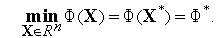
| (1) |
При решении задачи (1) методом с возвратом при неудачном шаге (одношаговый метод оптимизации) используется итерационная формула

| (2) |
где 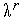 - величина шага на
- величина шага на 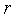 -ой итерации,
-ой итерации,  - реализация
- реализация 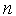 -мерного случайного вектора,
-мерного случайного вектора,  - некоторая векторная норма. Обычно в качестве координат вектора
- некоторая векторная норма. Обычно в качестве координат вектора 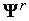 используют независимые случайные величины, равномерно распределенные в интервале
используют независимые случайные величины, равномерно распределенные в интервале 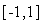 .
.
Схема метода с возвратом при неудачном шаге.
1. Задаем начальную точку  , начальную длину шага
, начальную длину шага 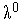 и полагаем счетчик числа итераций
и полагаем счетчик числа итераций 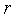 =0.
=0.
2. Задаем начальное значение счетчика числа неудачных попыток  =1.
=1.
3. Получаем реализацию случайных чисел 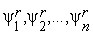 - компонент вектора
- компонент вектора 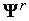 и по формуле (2) находим пробную точку
и по формуле (2) находим пробную точку  .
.
4. Вычисляем значение  (
(  ) функции
) функции  (
(  ) в точке
) в точке  .
.
5. Если 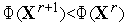 , то полагаем
, то полагаем  и переходим к п.3. Иначе – переходим к п.6.
и переходим к п.3. Иначе – переходим к п.6.
6. Полагаем  . Если
. Если 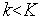 , то переходим к п.3. Иначе – переходим к п.7. Здесь
, то переходим к п.3. Иначе – переходим к п.7. Здесь  – предельное количество неудачных попыток (свободный параметр метода). Рекомендуется
– предельное количество неудачных попыток (свободный параметр метода). Рекомендуется 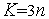 .
.
7. Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то полагаем 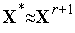 и завершаем итерации. Иначе – полагаем
и завершаем итерации. Иначе – полагаем  ,
, 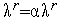 и переходим к п. 2. Здесь
и переходим к п. 2. Здесь 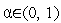 - коэффициент уменьшения шага (свободный параметр метода)
- коэффициент уменьшения шага (свободный параметр метода) 
В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций:
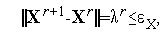
| (3) |
где 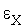 - константа, определяющая требуемую точность решения по
- константа, определяющая требуемую точность решения по  ;
;
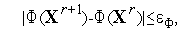
| (4) |
где 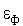 - константа, определяющая требуемую точность решения по
- константа, определяющая требуемую точность решения по  .
.
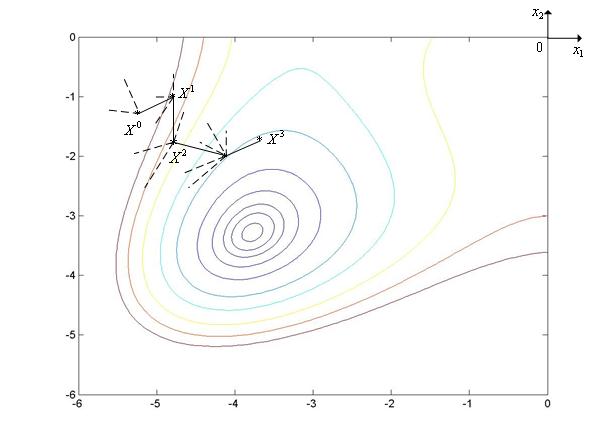
Метод с возвратом при неудачном шаге иллюстрирует рис. 1, на котором показан фрагмент линий уровня функции Химмельблау.
|
Рис. 1. Траектория поиска минимума функции Химмельблау методом с возвратом при неудачном шаге. Пунктиром на рисунке показаны неудачные шаги.
Модификацией метода с возвратом при неудачном шаге является метод наилучшей пробы (также одношаговый метод оптимизации).
Схема метода наилучшей пробы.
1. Задаем начальную точку  , начальную длину шага
, начальную длину шага 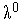 и полагаем счетчик числа итераций
и полагаем счетчик числа итераций 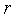 =0.
=0.
2. Генерируем  случайных векторов
случайных векторов 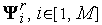 и по формуле (2) находим пробные точки
и по формуле (2) находим пробные точки 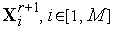
3. Вычисляем значения  (
( 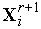 ) функции
) функции  (
(  ) в пробных точках
) в пробных точках 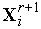 ,
,  [1,
[1,  ] и находим минимальное из этих значений
] и находим минимальное из этих значений
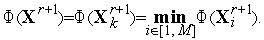
4. Если  (
( 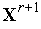 )<
)<  (
( 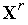 ), то полагаем
), то полагаем 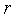 =
= 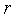 +1 и переходим к п.2. Иначе – переходим к п.5.
+1 и переходим к п.2. Иначе – переходим к п.5.
5. Проверяем условие окончания поиска (см. (3), (4)). Если условие окончания поиска выполнено, то полагаем 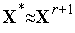 и завершаем итерации. Иначе – полагаем
и завершаем итерации. Иначе – полагаем 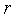 =
= 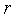 +1,
+1, 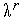 =
= 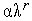 и переходим к п.2. Здесь
и переходим к п.2. Здесь 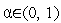 - коэффициент уменьшения шага (свободный параметр метода)
- коэффициент уменьшения шага (свободный параметр метода) 
Метод наилучшей пробы иллюстрирует рис. 2, на котором показан фрагмент линий уровня функции Химмельблау.
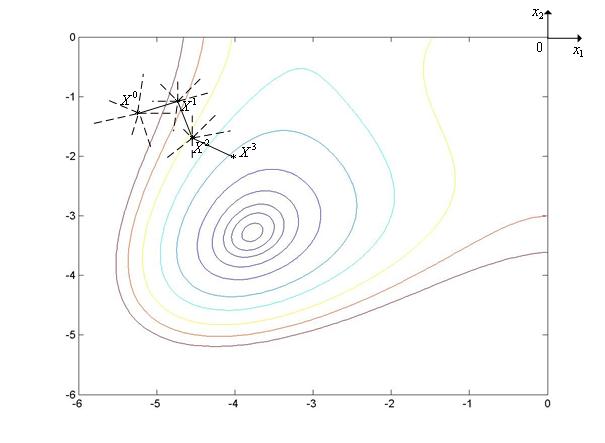
|
Рис. 2. Траектория поиска минимума функции Химмельблау методом наилучшей пробы. Пунктиром на рисунке показаны неудачные пробы.
8.2 Метод комплексов
Рассматривается следующая многомерная задача локальной безусловной оптимизации: найти минимум критерия оптимальности  (
(  ), определенного в
), определенного в  -мерном евклидовом пространстве
-мерном евклидовом пространстве  ,
,
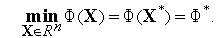
| (1) |
Комплексом называется многогранник с 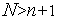 вершинами (не обязательно выпуклый). Рекомендуется
вершинами (не обязательно выпуклый). Рекомендуется 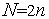 . Вообще говоря, комплексом в комбинаторной топологии называется геометрическая фигура, которая может быть разбита на более элементарные фигуры. В нашем случае такими элементарными фигурами являются симплексы. Поэтому, говоря более строго, в данном параграфе рассматриваются симплициальные комплексы.
. Вообще говоря, комплексом в комбинаторной топологии называется геометрическая фигура, которая может быть разбита на более элементарные фигуры. В нашем случае такими элементарными фигурами являются симплексы. Поэтому, говоря более строго, в данном параграфе рассматриваются симплициальные комплексы.
При решении задачи (1) методом комплексов используются следующие операции:
- генерация случайного комплекса;
- отражение вершины комплекса с растяжением;
- сжатие комплекса.
Генерация случайного комплекса. В пространстве  координаты вершин случайного комплекса с
координаты вершин случайного комплекса с  вершинами могут быть найдены по формуле
вершинами могут быть найдены по формуле
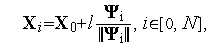
| (2) |
где  - произвольная начальная точка,
- произвольная начальная точка,  – номер вершины комплекса,
– номер вершины комплекса, 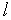 - скаляр, определяющий размеры комплекса,
- скаляр, определяющий размеры комплекса,  - реализация
- реализация 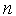 -мерного случайного вектора,
-мерного случайного вектора, 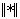 - некоторая векторная норма. Обычно в качестве координат вектора
- некоторая векторная норма. Обычно в качестве координат вектора  используют независимые случайные величины, равномерно распределенные в интервале
используют независимые случайные величины, равномерно распределенные в интервале 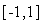
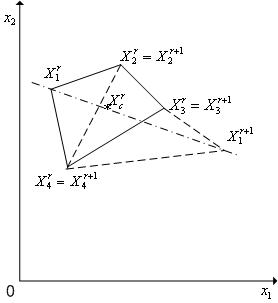
Отражение вершины комплекса с растяжением. Положим, что в пространстве  тем или иным способом задан комплекс
тем или иным способом задан комплекс 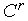 с
с  вершинами
вершинами 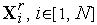 , и его вершину
, и его вершину 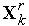 необходимо отразить через центр тяжести комплекса с растяжением. В новом комплексе
необходимо отразить через центр тяжести комплекса с растяжением. В новом комплексе 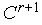 все вершины, кроме
все вершины, кроме  -ой, совпадают с соответствующими вершинами исходного комплекса
-ой, совпадают с соответствующими вершинами исходного комплекса 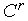 , а
, а  -я вершина находится на прямой, проходящей через центр тяжести этого комплекса и его вершину
-я вершина находится на прямой, проходящей через центр тяжести этого комплекса и его вершину 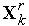 (см. рис. 1). Обозначим координаты вершин нового комплекса
(см. рис. 1). Обозначим координаты вершин нового комплекса 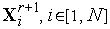 . Тогда имеем
. Тогда имеем
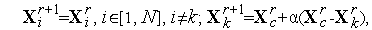
| (3) |
где  - коэффициент растяжения комплекса (рекомендуемое значение -
- коэффициент растяжения комплекса (рекомендуемое значение - 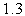 ),
), 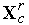 - вектор координат центра тяжести комплекса
- вектор координат центра тяжести комплекса 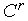 :
:
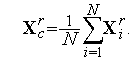
| (4) |
|
Рис. 1. Отражение вершины X1r комплекса Cr через центр его тяжести с растяжением. Пунктиром показан новый комплекс Cr+1.
Сжатие комплекса. Положим, что в пространстве  тем или иным способом задан комплекс
тем или иным способом задан комплекс  с
с  вершинами
вершинами  , и его вершину
, и его вершину  необходимо переместить ближе к центру тяжести комплекса
необходимо переместить ближе к центру тяжести комплекса 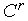 - выполнить сжатие комплекса. В новом комплексе
- выполнить сжатие комплекса. В новом комплексе 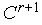 все вершины, кроме
все вершины, кроме  -ой, совпадают с соответствующими вершинами исходного комплекса
-ой, совпадают с соответствующими вершинами исходного комплекса 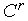 , а
, а  -я вершина находится на прямой, проходящей через центр тяжести этого комплекса и его вершину
-я вершина находится на прямой, проходящей через центр тяжести этого комплекса и его вершину 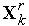 (см. рис. 2). Обозначим координаты вершин нового комплекса
(см. рис. 2). Обозначим координаты вершин нового комплекса 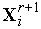 ,
,  [1,
[1,  ]. Тогда имеем
]. Тогда имеем
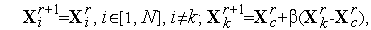
| (5) |
где  - коэффициент сжатия комплекса (рекомендуемое значение - 2),
- коэффициент сжатия комплекса (рекомендуемое значение - 2), 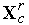 - вектор координат центра тяжести комплекса
- вектор координат центра тяжести комплекса 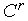 (см. (4)).
(см. (4)).

|
Рис. 2. Сжатие комплекса Cr Пунктиром показан новый комплекс Cr.
Схема простейшего варианта метода комплексов.
1. Задаем начальную точку 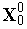 , исходя из которой должен быть построен комплекс
, исходя из которой должен быть построен комплекс 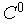 , начальное значение величины
, начальное значение величины 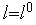 и полагаем счетчик числа итераций
и полагаем счетчик числа итераций 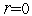 .
.
2. Генерируем  случайных векторов
случайных векторов 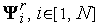 и по формуле (2) находим координаты
и по формуле (2) находим координаты 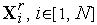 вершин комплекса
вершин комплекса 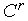 .
.
3. Вычисляем значения  (
( 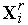 ) функции
) функции  (
(  ) во всех вершинах комплекса
) во всех вершинах комплекса 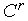 .
.
4. Находим максимальное из значений функции  (
(  ) в вершинах комплекса
) в вершинах комплекса 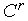
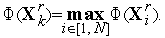
5. По формулам (3), (4) для комплекса 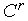 выполняем отражение вершины комплекса с растяжением
выполняем отражение вершины комплекса с растяжением 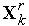 - получаем вершину
- получаем вершину 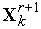 и новый комплекс
и новый комплекс 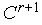 .
.
6. Вычисляем значение  (
( 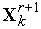 ) функции
) функции  (
(  ) в вершине
) в вершине 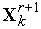 .
.
7. Если 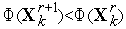 , то полагаем
, то полагаем 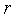 =
= 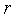 +1 и переходим к п.8. Иначе – по формулам (5), (4) выполняем сжатие симплекса
+1 и переходим к п.8. Иначе – по формулам (5), (4) выполняем сжатие симплекса 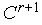 в направлении
в направлении 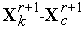 , полагаем
, полагаем  и переходим к п.6.
и переходим к п.6.
8. Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то в качестве точки 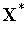 полагаем вершину комплекса
полагаем вершину комплекса 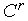 , к которой функция
, к которой функция  (
(  ) имеет наименьшее значение и завершаем итерации. Иначе – переходим к п. 4
) имеет наименьшее значение и завершаем итерации. Иначе – переходим к п. 4 
В качестве критерия окончания поиска может использоваться следующее условие: максимальная длина ребра комплекса 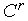 не превышает
не превышает 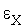 - требуемую точность решения по
- требуемую точность решения по  . Может использоваться также следующее аналогичное условие: максимальная разность значений функции
. Может использоваться также следующее аналогичное условие: максимальная разность значений функции  (
(  ) в двух вершинах комплекса
) в двух вершинах комплекса 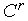 не превышает
не превышает 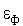 - требуемую точность решения по
- требуемую точность решения по  .
.
Могут использоваться также более сложные условия окончания поиска
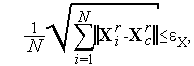
| (6) |
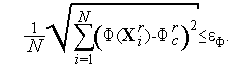
| (7) |
В формуле (6) векторная норма означает расстояние вершины 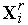 до центра тяжести комплекса
до центра тяжести комплекса 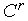 , а сама формула (6) определяет среднее расстояние вершин комплекса
, а сама формула (6) определяет среднее расстояние вершин комплекса 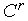 до его цента тяжести.
до его цента тяжести.
В формуле (7)  есть среднее значение функции
есть среднее значение функции  (
(  ) в вершинах комплекса
) в вершинах комплекса 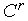 , а сама формула (7) определяет среднее отклонение значений функции
, а сама формула (7) определяет среднее отклонение значений функции  (
(  ) в вершинах комплекса
) в вершинах комплекса 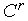 от этого среднего значения.
от этого среднего значения.
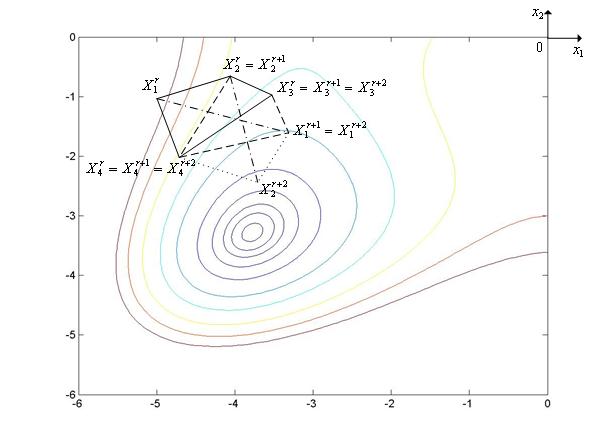
Метод комплексов иллюстрирует рис. 3, на котором показан фрагмент линий уровня функции Химмельблау. На рисунке исходный комплекс 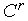 имеет вершины
имеет вершины 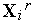 ,
,  [1, 4]. После отражения с растяжением вершины
[1, 4]. После отражения с растяжением вершины 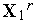 этого комплекса, в которой функция имеет максимальное значение, получаем комплекс
этого комплекса, в которой функция имеет максимальное значение, получаем комплекс 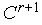 с вершинами
с вершинами 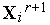 ,
,  [1, 4]. После отражения с растяжением вершины
[1, 4]. После отражения с растяжением вершины  комплекса
комплекса 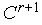 , в которой функция имеет максимальное значение, получаем комплекс
, в которой функция имеет максимальное значение, получаем комплекс 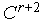 с вершинами
с вершинами 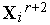 ,
,  [1, 4].
[1, 4].
|
Рис. 3. Траектория поиска минимума функции Химмельблау методом комплексов.
Известно множество модификаций рассмотренного метода комплексов, направленных, в частности, на преодоление «уплощения» комплекса в процессе поиска. С этой целью через фиксированное количество итераций находятся максимальная и минимальная диагонали комплекса и, если их отношение превышает заданное, то по рассмотренной схеме производится построение нового комплекса.
8.3 Метод повторяющегося случайного поиска
Рассматривается следующая многомерная задача локальной безусловной оптимизации: найти минимум критерия оптимальности  (
(  ), определенного в
), определенного в  -мерном евклидовом пространстве
-мерном евклидовом пространстве  ,
,
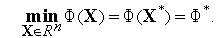
| (1) |
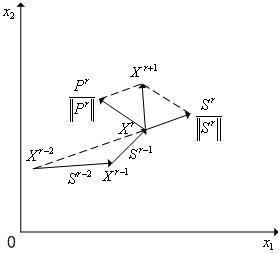
В методе повторяющегося случайного поиска (трех-шаговый метод) используется итерационная схема (см. рис. 1)
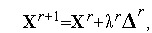
| (2) |
где 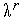 - величина шага (скаляр) на
- величина шага (скаляр) на 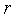 -ой итерации,
-ой итерации, 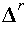 - (
- ( 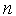 *1)-вектор, определяющий направление шага на
*1)-вектор, определяющий направление шага на 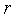 -ой итерации:
-ой итерации:
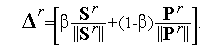
| (3) |
Здесь 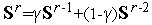 - вектор «предыстории», определяющий среднее направление поиска на двух предыдущих шагах;
- вектор «предыстории», определяющий среднее направление поиска на двух предыдущих шагах;  - некоторая векторная норма;
- некоторая векторная норма; 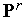 -
- 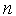 -мерный вектор псевдослучайных чисел, равномерно распределенных в интервале
-мерный вектор псевдослучайных чисел, равномерно распределенных в интервале 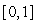 ; скаляр
; скаляр 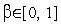 - коэффициент, задающий относительные веса детерминированной и случайной компонент в векторе
- коэффициент, задающий относительные веса детерминированной и случайной компонент в векторе 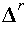 (свободный параметр метода); скаляр
(свободный параметр метода); скаляр 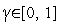 - коэффициент, задающий относительные веса векторов
- коэффициент, задающий относительные веса векторов 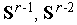 в векторе
в векторе 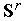 (свободный параметр метода).
(свободный параметр метода).
Заметим, что отношение  представляет собой единичный вектор направления
представляет собой единичный вектор направления 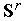 , а отношение
, а отношение 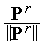 - единичный вектор направления
- единичный вектор направления 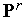 .
.
|
Рис. 1. К итерационной схеме метода повторяющегося случайного поиска.
Принято 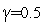 ,
, 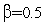 ,
, 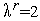 , так что
, так что 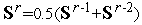 и
и 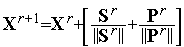 .
.
Упрощенная схема метода повторяющегося случайного поиска.
1. Задаем начальную точку  , начальный шаг
, начальный шаг 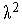 , значения коэффициентов
, значения коэффициентов  ,
,  и полагаем счетчик числа итераций
и полагаем счетчик числа итераций 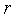 =2.
=2.
2. Тем или иным способом, например, с помощью одношагового метода наилучшей пробы определяем точки  ,
,  - этап «разгона» метода.
- этап «разгона» метода.
3. Генерируем 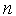 -мерный случайный вектор
-мерный случайный вектор 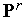 и по формулам (2), (3) вычисляем координаты точки
и по формулам (2), (3) вычисляем координаты точки  и значение
и значение  (
(  ) функции
) функции  (
(  ) в этой точке.
) в этой точке.
4. Если 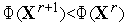 , то проверяем условие окончания итераций (см. ниже). Если условие окончания выполнено, то полагаем
, то проверяем условие окончания итераций (см. ниже). Если условие окончания выполнено, то полагаем 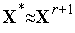 и завершаем итерации. Если условие окончания итераций не выполнено, то некоторому правилу увеличиваем длину шага
и завершаем итерации. Если условие окончания итераций не выполнено, то некоторому правилу увеличиваем длину шага 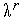 , например, полагая
, например, полагая  , принимаем
, принимаем  и переходим к п.3. Если
и переходим к п.3. Если  , то переходим к п. 5.
, то переходим к п. 5.
5. Некоторое фиксированное количество раз делаем попытку, исходя из той же точки  , не меняя длины шага
, не меняя длины шага 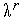 , добиться уменьшения значения функции
, добиться уменьшения значения функции  (
(  ) путем только изменения вектора
) путем только изменения вектора 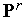 , т.е., не меняя
, т.е., не меняя  и
и 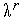 , переходим на п. 3. Если это фиксированное количество попыток не привело к успеху, то, исходя из той же точки
, переходим на п. 3. Если это фиксированное количество попыток не привело к успеху, то, исходя из той же точки  ,по некоторому правилу уменьшаем длину шага
,по некоторому правилу уменьшаем длину шага 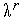 , например, полагая
, например, полагая  , и переходим к п.3
, и переходим к п.3 
В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций

где 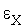 - константа, определяющая требуемую точность решения по
- константа, определяющая требуемую точность решения по  ;
;

где 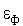 - константа, определяющая требуемую точность решения по
- константа, определяющая требуемую точность решения по  .
.
Известно множество модификаций рассмотренной простейшей схемы метода повторяющегося случайного поиска. Например, в процессе поиска могут изменяться по некоторым правилам не только длина шага 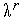 , но и коэффициенты
, но и коэффициенты  ,
,  .
.
Метод повторяющегося случайного поиска иллюстрирует рис. 2, на котором показан фрагмент линий уровня функции Химмельблау.

|
Рис. 2. Траектория поиска минимума функции Химмельблау методом повторяющегося случайного поиска.
На рисунке принято  ,
,  ,
, 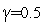 ,
, 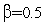 ,
, 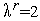 , так что
, так что 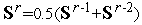 и
и  . Пунктиром показаны отвергнутые векторы
. Пунктиром показаны отвергнутые векторы  .
.
8.4 Метод случайного поиска с постоянным радиусом поиска и случайными направлениями
Рассматривается следующая многомерная задача локальной безусловной оптимизации: найти минимум критерия оптимальности  (
(  ), определенного в
), определенного в 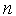 -мерном евклидовом пространстве
-мерном евклидовом пространстве  ,
,
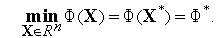
| (1) |
Метод случайного поиска с постоянным радиусом поиска и случайными направлениями использует процедуру генерации случайных точек, равномерно распределенных по поверхности гиперсферы в пространстве  . Пусть
. Пусть  - вектор координат центра гиперсферы,
- вектор координат центра гиперсферы,  - радиус гиперсферы,
- радиус гиперсферы,  - вектор с началом в точке
- вектор с началом в точке  и концом в искомой точке на поверхности гиперсферы,
и концом в искомой точке на поверхности гиперсферы,  - углы между вектором
- углы между вектором  и ортами координатных осей
и ортами координатных осей  .
.
Во введенных обозначениях схема алгоритма генерации случайных точек, равномерно распределенных по поверхности гиперсферы радиуса  , может быть представлена в следующем виде:
, может быть представлена в следующем виде:
- генерируем
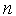 случайных чисел, равномерно распределенных в интервале
случайных чисел, равномерно распределенных в интервале  ;
; - вычисляем направляющие косинусы
 вектора
вектора  ;
; - находим координаты искомой точки
 .
.
Упрощенная схема метода случайного поиска с постоянным радиусом поиска и случайными направлениями.
1. Задаем начальную точку  , начальный радиус гиперсферы
, начальный радиус гиперсферы  , и полагаем счетчик числа итераций
, и полагаем счетчик числа итераций 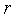 =0.
=0.
2. Генерируем случайные точки 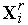 ,
,  [1,
[1,  ] равномерно распределенные по поверхности гиперсферы радиуса
] равномерно распределенные по поверхности гиперсферы радиуса  с центром в точке
с центром в точке  . Здесь
. Здесь  – количество точек – свободный параметр метода.
– количество точек – свободный параметр метода.
3. Вычисляем значения минимизируемой функции  (
( 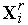 ) в полученных точках и находим точку, в которой достигается минимальное значение функции
) в полученных точках и находим точку, в которой достигается минимальное значение функции  (
(  ):
):
