Расчет индуктивности цилиндрической катушки

Определим индуктивность круглой цилиндрической однослойной катушки длиной 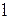по известным радиусу катушки 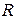и числу витков обмотки .

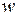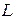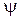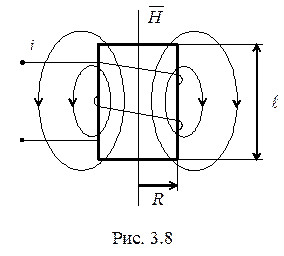
Индуктивность катушки может быть найдена как отношение полного потокосцепления к току катушки. Основная трудность решения этой задачи состоит в расчете величины потокосцепления 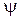катушки, так как различные магнитные силовые линии сцепляются с различным числом витков (рис.3.8).

Упростим постановку задачи, предполагая в первом приближении катушку бесконечно длинной и считая, что ее витки намотаны вплотную друг к другу. При этом можно считать магнитное поле сосредоточенным внутри катушки, а силовые линии - замыкающимися в бесконечности (рис.3.9).

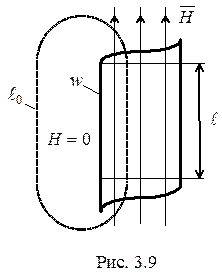Если длина реальной катушки значительно превосходит ее диаметр, то картину магнитного поля такой катушки можно приближенно считать близкой к изображенной на рис.3.9. Напряженность магнитного поля 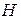определим из закона полного тока, выбрав контур интегрирования 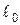так, чтобы часть его проходила внутри катушки параллельно ее оси. Поскольку предполагается, что вне катушки , можно записать

 

и напряженность магнитного поля внутри катушки . Магнитный поток сквозь сечение катушки равен

и так как потокосцепление , окончательно получаем

Подчеркнем еще раз, что эта формула для определения индуктивности является приближенной и справедлива для однослойных катушек, длина которых значительно превосходит диаметр.