Интерполяционная формула Лагранжа

Для произвольно заданных узлов интерполирования пользуются более общей формулой, называемой интерполяционным многочленом Лагранжа.

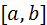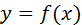Пусть на отрезке даны n+1 различных значений аргумента: и известны для функции соответствующие значения: . Требуется построить полином степени не выше n, имеющий в заданных узлах те же значения, что и функция 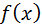, т.е. такой что (рис.1)

Интерполяционная формула Лагранжа имеет вид:

Если узлы интерполирования – равноотстоящие, то интерполяционный полином Лагранжа совпадает с соответствующим интерполяционным полиномом Ньютона.