Асимптотический анализ функций
Скорости роста и их классификация.
Наиболее важным при анализе алгоритмов является скорость роста количества операций при возрастании объема входных данных. Это называется скоростью роста алгоритма. Интересно изучить, как поведет себя алгоритм при увеличении объема данных. Скорость роста разных функций при увеличении объема входных данных различна. При малых объемах входных данных разница между функциями практически мало заметна, но при больших объемах входных данных мы можем выделить быстро растущие функции и функции с медленным ростом.
Для описания скорости роста функции используют О- символику.
Когда мы говорим, что функция трудоемкости fA(D) некоторой программы имеет порядок О(n2), где n=|D|, то это значит, что существуют положительные константы с и n0 такие, что для всех n, больших или равных n0, выполняется неравенство fA(n)<=cn2. . Для программ, у которых время выполнения имеет порядок O(f(n)) , говорят, что они имеют порядок (степень) роста f(n).Это значит, что f(n) является верхней границей скорости роста fA(n).
Для указания нижней границы скорости роста fA(n) используем обозначение
(g(n)). Это означает, что функция g(n) является нижней границей скорости роста fA(n).
Скорость роста определяется старшим членом формулы. Так как младшие растут медленно, ими можно пренебречь. Отбросив младшие члены, получаем то, что принято называть порядком функции или алгоритма. Алгоритмы таким образом можно группировать по скорости роста их сложности.
Алгоритмы по скорости роста их сложности сгруппированы в три категории:
· Алгоритмы, сложность которых растет по крайней мере так же быстро, как и данная функция.
· Алгоритмы, сложность которых растет с той же скоростью
· Алгоритмы, сложность которых растет медленнее, чем эта функция.
Класс функций 
(f) . (омега большое) (функция, принадлежащая этому классу, ограничена снизу функцией f)
Функция g принадлежит этому классу, если при всех значениях аргумента n , больших некоторого порога no значение g(n) > c*f(n) для некоторого положительного числа с. Класс задается указанием своей нижней границы. А это значит, что в класс (n2) входят все функции, растущие быстрее, чем n2 ( n3 или 2n ).Этот класс мало интересен, если говорить об эффективности алгоритма.
Если есть функция f(n) и функция cg(n) , то
( то есть функция g(n) лежит под кривой f(n))
Класс функций O(f) ( О большое) (функция, принадлежащая этому классу, ограничена сверху функией f)
Этот класс состоит из функций, растущих не быстрее f .Функция f образует верхнюю границу для класса. Функции g принадлежит классу О(f), если g(n) <= c*f(n) для всех n, больших некоторого порога n0 , и для некоторой положительной константы с. Это важно для нас. У нас есть два алгоритма. Принадлежит ли сложность первого из них классу О большое от сложности второго. Если окажется, что это так, значит, второй алгоритм не лучше первого решает поставленную задачу.
( оценка O требует только, чтобы функция f(n) не превышала g(n), начиная с n>n0, с точностью до постоянного множителя:
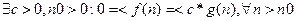(то есть функция f(n) не должна превышать g(n) , начиная с n>n0,с точностью до постоянного множителя.)
Класс 
(f) (тета большое) (функция, принадлежащая этому классу, ограничена снизу и сверху функцией f)
Это класс функций, растущих с той же скоростью, что и f. Этот класс представляет собой пересечение двух предыдущих классов,
(f) = (f) 
O(f)
При сравнении алгоритмов нас будут интересовать такие, которые решают задачу быстрее, чем уже изученные. Алгоритмы этого класса не очень интересны.
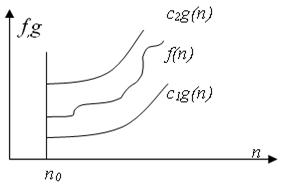
(f(n)= 
, если существуют положительные c1,c2,n0, такие, что c1*g(n)=<f(n)=<c2*g(n), при n>n0.) Обычно говорят, что при этом функция g(n) является асимптотически точной оценкой функции f(n), так как по определению функция f(n) не отличается от функции g(n) с точностью до постоянного множителя. При этом из f(n)= следует , что g(n)= 
Самый для нас интересный класс О. Проверить принадлежность функции классу О(f) можно либо с помощью данного выше определения, либо так:
g 
O(f), если 
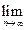
= c для некоторой константы с.
Это означает, что если предел отношения g(n)/f(n) существует и он меньше бесконечности, то g O(f). Это не просто проверить для некоторых функций. В таких случаях по правилу Лопиталя (раскрывающего неопределенности вида ноль на ноль или бесконечность на бесконечность) можно заменить предел самих функций пределом их производных.
Каждый из классов является множеством, поэтому имеет смысл выражение “g – элемент этого множества”. И когда мы пишем g=O(f) , то это значит g O(f).
Итак, в асимптотическом анализе используются обозначения, позволяющие показать скорость роста функции : (классификация скоростей роста сложности алгоритмов)
1. Оценка 
(тетта)
2. Оценка О (О большое)
3. Оценка 
(Омега)
Эти классы описаны выше.
Примеры:
Оценка
1. f(n)=4 n2 +n ln(n)+174 f(n)= (n2)
2. f(n)= (1)- запись означает, что f(n) или равна константе, не равной 0, или f(n) ограничена константой на бесконечности:
f(n)=7+1/n = (1).
Оценка О
f(n)=1/n; f(n)=12; f(n)=3n+17; f(n)=n ln(n); f(n)=6n2 +24n +77
для всех этих функций справедлива оценка О(n2)
Оценка
Теорема Для любых двух функций f(n) и g(n) соотношение f(n) = (g(n)) выполняется тогда и только тогда, когда f(n)=O(g(n)) и f(n)= (g(n)).
Например, (n ln(n)) обозначает класс функций, которые растут не медленнее, чем g(n)=n ln(n)). В этот класс попадают все полиномы со степеньюn n , больше двух и все степенные функции с основанием, большим единицы.
Таким образом, в асимптотическом анализе алгоритмов разработаны специальные методы получения асимптотических оценок.
Классификация алгоритмов по трудоёмкости О().
О (1)
Большинство инструкций программы запускается один или несколько раз, независимо от n. Т.е. время выполнения программы постоянно
О (n)
Время выполнения программы линейно зависит от n. Каждый входной элемент подвергается небольшой обработке.
(поиск min/max в массиве, значения в связанном списке) (for…; i<n ;...)
О (n2)
Время выполнения программы является квадратичным. Такие алгоритмы можно использовать для относительно небольших n. Такое время характерно, когда обрабатываются все пары элементов (в цикле двойного уровня вложенности).
(сортировки выбором, вставками)
О (n3)
Алгоритм обрабатывает тройки элементов (возможно, в цикле тройного уровня вложенности) и имеет кубическое время выполнения. Такой алгоритм практически применим только для малых задач. (умножение матриц)
О (log n)
Программа работает медленнее с ростом n. Такое время характерно для программ, которые сводят большую задачу к набору меньших подзадач, уменьшая на каждом шаге размер подзадачи на некоторый постоянный коэффициент. Общее решение находится в одной из подзадач. Логарифмическая зависимость. (бинарный поиск)
О (n*log n)
Время выполнения программы пропорционально n*log n возникает тогда, когда алгоритм решает задачу, разбивая ее на меньшие подзадачи, решая их независимо и затем объединяя решения подзадач (комбинация).
(сортировки быстрая, слиянием)
О (2n)
Лишь несколько алгоритмов с экспоненциальным временем имеет практическое применение, хотя такие алгоритмы возникают естественным образом при попытке прямого решения задач. (перебор и сравнение различных решений) Для комбинаторных задач нереализуемы. Сведение к приближенному алгоритму с приближенным значением.
Обычно время выполнения в результате анализа выглядит как многочлен, где главным членом является один из вышеприведенных. Коэффициент при главном члене зависит от количества инструкций во внутреннем цикле. Поэтому так важно максимально упрощать количество инструкций во внутреннем цикле. При росте N начинает доминировать главный член, поэтому остальными слагаемыми в многочлене можно пренебречь.
Выводы:
Итак, общее количество операций, выполняемых алгоритмом, не играет существенной роли при анализе алгоритмов. А вот скорость роста этого числа при возрастании объема входных данных очень важна. Она - то и называется скоростью роста алгоритма.
Зная такие оценки для разных алгоритмов решения какой-либо задачи, мы получаем возможность сравнивать эти алгоритмы с точки зрения их эффективности. Однако асимптотические оценки дают нам только порядок функции, а сами результаты сравнения справедливы только при очень больших размерах входа.
В реальной работе важно знать среднее количество операций, совершаемых алгоритмом. Здесь обычно рассматриваются три случая :
· Худший - для наибольшего количества операций, совершаемых алгоритмом для решения конкретных проблем размерности n.
· Лучший - для наименьшего количества операций совершаемых алгоритмом для решения конкретных проблем размерности n.
· Средний -для среднего количества операций, совершаемых алгоритмом для решения конкретных проблем размерности n.
Конкретная проблема представляет собой упорядоченное множество элементов (слов). При решении на компьютерах практических задач возникает вопрос о границах практического применения данного алгоритма решения задачи в смысле ограничения на ее размерность.
Замечание: Асимптотический анализ
Часто приходится решать задачу сравнения алгоритмов для определения того, насколько быстро они действуют или сколько памяти для них требуется. Есть два пути . Один – эталонный тест- прогон программы на компьютере и измерение быстродействия в секундах и потребление памяти в байтах. Но при этом мы измеряем производительность конкретной программы, написанной на конкретном языке, работающей на конкретном компьютере с конкретным компилятором и конкретными входными данными. При этом нам трудно будет предсказать, насколько успешно будет действовать наш алгоритм в случае использования другого компьютера, другого компилятора или другого набора исходных данных.
1. Алгоритмы обычно не поддаются точному анализу. Тогда прибегают к аппроксимации. Например, говорят, что быстродействие некоторого алгоритма, например, программы вычисления суммы последовательности чисел характеризуется величиной O(n), где n –длина последовательности. Это значит, что быстродействие алгоритма измеряется величиной , пропорциональной n , возможно, за исключением нескольких небольших значений n. Перейдя к использованию системы обозначений О( ), мы получаем возможность воспользоваться так называемым асимптотическим анализом. Это дает нам основания утверждать, что если n асимптотически приближается к бесконечности, то алгоритм, характеризующийся показателем О(n) , проявит себя лучше, чем алгоритм О(n2). Однако, единственное число, полученное с помощью эталонного тестирования, не может служить обоснованием подобного утверждения.
2. Система обозначений О() позволяет создать абстрактное представление, в котором не учитываются постоянные коэффициенты, благодаря чему она становится более простой в использовании, но менее точной, чем когда вы измеряете общее количество шагов, выполняемых алгоритмом.
3. Асимптотический анализ представляет собой инструментальное средство, наиболее широко используемое для анализа алгоритмов. Система обозначений О() представляет собой хороший компромисс между точностью и простотой анализа.
С помощью системы обозначений О() мы получаем возможность рассуждать об эффективности конкретного алгоритма. Но мы ничего не узнаем о возможности существования лучшего алгоритма для рассматриваемой задачи. Для исследования самих задач, а не алгоритмов их решения существует анализ сложности. Именно здесь проводится водораздел между задачами, которые могут быть решены за время, измеряемое полиномиальным соотношением, и задачами которые не могут быть решены за время, измеряемое полиномиальными соотношениями, независимо от того, какой алгоритм для этого используется. Класс полиномиальных задач, которые могут быть решены за время О(nk) для некоторого k обозначают как Р. ( O(log n) и O(n))