Виды кривых распределения.

Как видно из рис. 4.1. кривая распределения имеет колоколообразный и вид. Наибольшее количество случаев дает реализации вблизи центра распределения, а чем больше отклонения от центра, тем меньше вероятность их по­явления. При ограниченном числе испытаний можно вы­делить наибольшую и наиме­ньшую реализации случайной величины. Однако при увели­чении числа испытаний край­ние реализации все более уда­ляются от центра. Теоретиче­ски можно представить, что кривая распределения уходит в бесконечность с одной или с обеих сторон.

Наиболее часто применяется теоретическая кривая распределе­ния, описываемая уравнением

(4.9)

Это распределение называется нормальным, или гаус­совым, и имеет вид, показанный на рис. 4.1. Коэффициент 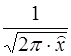вводится для того, чтобы площадь кривой распределения была равна единице, 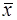и представляют собой здесь центр и диспер­сию нормального распределения. Кривая (4.9) уходит в бесконеч­ность в обе стороны от центра с очень быстро затухающими орди­натами.

Интегральная кривая нормального распределения выражается формулой

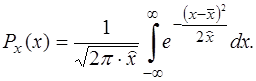(4.10)

Введя новую переменную под знаком интеграла

(4.11)

эту формулу можно преобразовать к виду

(4.12)

где

(4.13)

— интеграл вероятности Гаусса. Для этого интеграла в справочни­ках имеются подробные таблицы. Некоторые значения ординат кривых нормального распределения Рх в функции от даны в табл. 4.1.

Таблица 4.1

g 1,28 2,32 3, 15 3,77 4,00 4,50 5,00
Рх 0,1 0,01 0,001 0,0001 3,2×10-5 3×10-6 2,9×10-7

 

Для величин, которые не могут принимать отрицательных зна­чений, применяются различные асимметричные кривые распределе­ния. Однако во многих случаях для этих величин можно использо­вать и нормальное распределение при условии, что центр распределения отстоит от нуля на несколько стандартов , тогда вероятность отрицательных значений будет нич­тожно малой и ею можно пренебречь.

Для всякой интегральной кривой распределения Рх (х) можно построить обратную функцию зависимости х от Рх. При этом зна­чения х называются квантилями вероятности Рх.