Переменный электрический ток
§ 40 Токи в цепях с конденсаторами и индуктивностями
Рассмотрим переходные процессы, которые протекают при подключении к источнику тока конденсатора или индуктивности (рис.40.1). В параграфах 40-42 будем записывать все уравнения в СИ, в конце 42 параграфа вернемся в Гауссову систему для определения скорости бегущей в линии волны.
Рис.40.1

При подключении конденсатора в произвольный момент времени ЭДС источника равна сумме падения напряжения на резисторе, через который течет ток зарядки конденсатора, и напряжения на конденсаторе:
 .
.
Заряд в определении силы тока и заряд конденсатора – одна и та же переменная, поскольку заряд 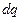 , протекающий через сечение проводника за время
, протекающий через сечение проводника за время 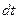 , оказывается на обкладке конденсатора и меняет ее заряд ровно на такую же величину. Решение неоднородного уравнения с постоянной правой частью
, оказывается на обкладке конденсатора и меняет ее заряд ровно на такую же величину. Решение неоднородного уравнения с постоянной правой частью

можно получить, сделав замену переменной  . Тогда получим однородное уравнение
. Тогда получим однородное уравнение
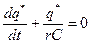 .
.
Его решение:  . Постоянную интегрирования найдем из начальных условий
. Постоянную интегрирования найдем из начальных условий  :
:  . Тогда зависимость заряда конденсатора от времени будет экспоненциальной:
. Тогда зависимость заряда конденсатора от времени будет экспоненциальной:
 . (40.1)
. (40.1)
Если обкладки заряженного конденсатора с зарядом  соединить через резистор
соединить через резистор  , то конденсатор начнет разряжаться. В произвольный момент времени напряжение на нем будет равно падению напряжения на резисторе:
, то конденсатор начнет разряжаться. В произвольный момент времени напряжение на нем будет равно падению напряжения на резисторе:  . Поскольку
. Поскольку  , получим дифференциальное уравнение
, получим дифференциальное уравнение  , которое необходимо поправить, добавив знак минус в том случае, если
, которое необходимо поправить, добавив знак минус в том случае, если 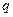 в левой и правой частях уравнения одна и та же переменная (заряд конденсатора в решаемой задаче уменьшается). Решая уравнение
в левой и правой частях уравнения одна и та же переменная (заряд конденсатора в решаемой задаче уменьшается). Решая уравнение  для начальных условий
для начальных условий  , получим:
, получим:
 . (40.2)
. (40.2)
Характеристическое время  , в течение которого заряд уменьшается в e раз, называется постоянной времени
, в течение которого заряд уменьшается в e раз, называется постоянной времени  цепочки.
цепочки.
При подключении индуктивности к источнику (рис.40.1b), решая аналогичную задачу, получим следующую временную зависимость тока через индуктивность:
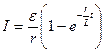 (40.3)
(40.3)
Очень важную практическую проблему приходится решать при размыкании цепи постоянного тока с большой индуктивностью. Такая цепь, например, - цепь питания постоянного электромагнита. Поскольку его обмотка содержит много витков и намотана она на сердечнике с большим значением магнитной проницаемости, при выключении может возникнуть очень большая ЭДС индукции 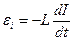 . Если в цепи с индуктивностью 1Гн ток в 1А выключается за 1 мкс, то возникшая ЭДС будет равна миллиону вольт. Естественно, что гораздо раньше воздушный промежуток пробивается, и возникает между контактами ключа разряд. Время выключения при этом увеличивается. Даже в вакууме таких перенапряжений не возникает за счет автоэлектронной эмиссии.
. Если в цепи с индуктивностью 1Гн ток в 1А выключается за 1 мкс, то возникшая ЭДС будет равна миллиону вольт. Естественно, что гораздо раньше воздушный промежуток пробивается, и возникает между контактами ключа разряд. Время выключения при этом увеличивается. Даже в вакууме таких перенапряжений не возникает за счет автоэлектронной эмиссии.
Один из способов уменьшения перенапряжения после выключения тока через индуктивность – включение параллельно ей сопротивления  (рис.40.1с). При размыкании ключа К (до этого момента считаем, что ток через индуктивность уже установился и стал равен предельному значению
(рис.40.1с). При размыкании ключа К (до этого момента считаем, что ток через индуктивность уже установился и стал равен предельному значению  ) ток потечет через резистор
) ток потечет через резистор  , ток через индуктивность будет меняться, возникнет ЭДС индукции, которая будет равна падению напряжения на резисторе
, ток через индуктивность будет меняться, возникнет ЭДС индукции, которая будет равна падению напряжения на резисторе  .
.
Рис.40.2
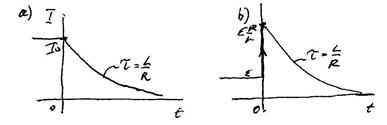
Решая это дифференциальное уравнение с начальным условием  , получим зависимость тока через индуктивность от времени (рис.40.2а):
, получим зависимость тока через индуктивность от времени (рис.40.2а):
 , (40.4)
, (40.4)
где  - постоянная времени, в течение которого ток уменьшается в
- постоянная времени, в течение которого ток уменьшается в  раз. ЭДС индукции, возникающая в контуре
раз. ЭДС индукции, возникающая в контуре  при выключении, будет равна:
при выключении, будет равна:  . В начальный момент времени при выключении напряжение на индуктивности скачком изменится от
. В начальный момент времени при выключении напряжение на индуктивности скачком изменится от 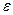 источника до
источника до 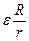 (рис.40.2b), затем будет экспоненциально спадать.
(рис.40.2b), затем будет экспоненциально спадать.
В заключение анализа  цепей рассмотрим интегрирующую и дифференцирующую
цепей рассмотрим интегрирующую и дифференцирующую  - цепочки. Если переменное напряжение
- цепочки. Если переменное напряжение  подать на последовательно соединенные резистор с сопротивлением
подать на последовательно соединенные резистор с сопротивлением  и конденсатор с емкостью
и конденсатор с емкостью  , то напряжение на конденсаторе (рис.40.3а) будет пропорционально интегралу по времени от
, то напряжение на конденсаторе (рис.40.3а) будет пропорционально интегралу по времени от  , а напряжение на резисторе (рис.40.3b) будет пропорционально производной по времени входного напряжения.
, а напряжение на резисторе (рис.40.3b) будет пропорционально производной по времени входного напряжения.
Рис.40.3

Для интегрирующей цепочки пусть напряжение на входе меняется по гармоническому закону 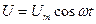 . Найдем напряжение на выходе, перейдя к дифференциальному уравнению с комплексными переменными.
. Найдем напряжение на выходе, перейдя к дифференциальному уравнению с комплексными переменными. 

 :
:


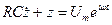 .
.
Вклад в решение этого уравнения, который дает решение соответствующего однородного уравнения мы уже нашли (40.1). Ищем частное решение неоднородного уравнения в виде  . После подстановки этой функции в дифференциальное уравнение получаем:
. После подстановки этой функции в дифференциальное уравнение получаем:
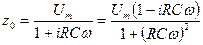 .
.
Амплитуда колебаний напряжения на конденсаторе  будет равна
будет равна  :
:
 .
.
Результат интегрирования будет тем ближе к точному значению (в данном случае это ноль), чем больше постоянная времени  - цепочки будет превышать период колебаний напряжения на входе
- цепочки будет превышать период колебаний напряжения на входе  . Другой, более интересный, пример интегрирования для напряжения на входе, меняющегося по закону
. Другой, более интересный, пример интегрирования для напряжения на входе, меняющегося по закону  даст нам следующий результат интегрирования:
даст нам следующий результат интегрирования:
 ,
,
который совпадает с правильным значением при  . Вклад в общее решение неоднородного уравнения, который дает решение соответствующего однородного уравнения экспоненциально спадает со временем. Процесс изменения напряжения на конденсаторе иллюстрирует рис.40.4.
. Вклад в общее решение неоднородного уравнения, который дает решение соответствующего однородного уравнения экспоненциально спадает со временем. Процесс изменения напряжения на конденсаторе иллюстрирует рис.40.4.
Рис.40.4

Для дифференцирующей цепочки из уравнения  получим после дифференцирования по времени уравнение
получим после дифференцирования по времени уравнение  , аналогичное только что решенному с той разницей, что в правой части производная входного напряжения. Качественно проанализируем дифференцирование прямоугольных импульсов. На рисунке 40.5 показан один прямоугольный импульс, длительности переднего и заднего фронтов которого для простоты считаем одинаковыми и равными
, аналогичное только что решенному с той разницей, что в правой части производная входного напряжения. Качественно проанализируем дифференцирование прямоугольных импульсов. На рисунке 40.5 показан один прямоугольный импульс, длительности переднего и заднего фронтов которого для простоты считаем одинаковыми и равными  . Призводная этого импульса приведена ниже и представляет собой два прямоугольных импульса одинаковой амплитуды и противоположной полярности. Каждый из этих импульсов эквивалентен включению в нашей схеме источника постоянного напряжения на время равное
. Призводная этого импульса приведена ниже и представляет собой два прямоугольных импульса одинаковой амплитуды и противоположной полярности. Каждый из этих импульсов эквивалентен включению в нашей схеме источника постоянного напряжения на время равное  .
.
Рис.40.5

При включении источника ток нарастает по экспоненте. На третьем графике внизу видна начальная, почти линейная, часть этого нарастания. Затем ток спадает до нуля с постоянной времени  (считаем, что внутреннее сопротивление источника мало). Для отрицательного импульса наблюдается то же самое.
(считаем, что внутреннее сопротивление источника мало). Для отрицательного импульса наблюдается то же самое.
§ 41 Колебания в LC-контуре
Рассмотрим цепь, состоящую из последовательно соединенных резистора  , конденсатора
, конденсатора  и индуктивности
и индуктивности  , которую можно подключать к источнику постоянного тока, закоротить, или подключать к источнику переменного напряжения, меняющегося по гармоническому закону (рис.41.1).
, которую можно подключать к источнику постоянного тока, закоротить, или подключать к источнику переменного напряжения, меняющегося по гармоническому закону (рис.41.1).
Рис.41.1

Подключим к цепи источник постоянного тока. После завершения переходных процессов конденсатор зарядится до максимального заряда  . Затем в момент времени
. Затем в момент времени  отключим источник и закоротим контур. В произвольный момент времени сумма падения напряжения на резисторе и напряжения на конденсаторе будет равна ЭДС индукции, возникающей в индуктивности:
отключим источник и закоротим контур. В произвольный момент времени сумма падения напряжения на резисторе и напряжения на конденсаторе будет равна ЭДС индукции, возникающей в индуктивности:

 .
.
Для заряда конденсатора из этого уравнения получим следующее однородное дифференциальное уравнение второго порядка:
 .
.
Это уже знакомое нам (Механика, 19.3) уравнение гармонического осциллятора с затуханием. После подстановки  получаем характеристическое уравнение
получаем характеристическое уравнение  , корни которого:
, корни которого:
 .
.
Если  , то наблюдаем быстро затухающий апериодический процесс
, то наблюдаем быстро затухающий апериодический процесс
 . (41.1)
. (41.1)
Постоянные интегрирования  определим из начальных условий
определим из начальных условий  и
и  :
:
 . (41.2)
. (41.2)
Заряд конденсатора меняется в этом случае со временем так, как показано на рис.41.1.
Если  , то корни характеристического уравнения мнимые, и мы получаем решение в виде:
, то корни характеристического уравнения мнимые, и мы получаем решение в виде:
 ,
,
где постоянные интегрирования  определяются аналогично (41.2), только знак выражения под корнем противоположный. Если
определяются аналогично (41.2), только знак выражения под корнем противоположный. Если  , то
, то  и окончательное решение мы можем записать в виде:
и окончательное решение мы можем записать в виде:
 , (41.3)
, (41.3)
где  - коэффициент затухания, а
- коэффициент затухания, а  - частота собственных колебаний в
- частота собственных колебаний в  - контуре с затуханием. Использовав связь
- контуре с затуханием. Использовав связь  , получим уравнение аналогичное (41.3), которое будет описывать колебания напряжения на конденсаторе. Их мы можем наблюдать на экране осциллографа (рис.41.2)
, получим уравнение аналогичное (41.3), которое будет описывать колебания напряжения на конденсаторе. Их мы можем наблюдать на экране осциллографа (рис.41.2)
Рис.41.2

Если пренебречь затуханием, которое обусловлено джоулевыми потерями энергии в сопротивлении  , посчитав его равным нулю, то собственная частота колебаний в идеальном
, посчитав его равным нулю, то собственная частота колебаний в идеальном  - контуре будет равна
- контуре будет равна  .
.
Напомню другие характеристики гармонического осциллятора с малым затуханием: логарифмический декремент затухания
 ; (41.4)
; (41.4)
добротность осциллятора, которая в случае  - контура с затуханием будет равна:
- контура с затуханием будет равна:
 . (41.5)
. (41.5)
Вынужденные колебания в  - контуре мы будем наблюдать, если подключим его к источнику переменного напряжения (рис.41.1). В этом случае контур будет называться последовательным контуром. Если через резистор
- контуре мы будем наблюдать, если подключим его к источнику переменного напряжения (рис.41.1). В этом случае контур будет называться последовательным контуром. Если через резистор  к источнику подключить параллельно соединенные емкость и индуктивность, то такой контур будет называться параллельным контуром.
к источнику подключить параллельно соединенные емкость и индуктивность, то такой контур будет называться параллельным контуром.
Пусть напряжение источника меняется по гармоническому закону  . Дифференциальное уравнение, описывающее колебания заряда (или напряжения) конденсатора, будет полностью совпадать с уже решенным нами дифференциальным уравнением для вынужденных колебаний гармонического осциллятора (20.2, Механика):
. Дифференциальное уравнение, описывающее колебания заряда (или напряжения) конденсатора, будет полностью совпадать с уже решенным нами дифференциальным уравнением для вынужденных колебаний гармонического осциллятора (20.2, Механика):
 , (45.6)
, (45.6)
где  .
.
Амплитуда установившихся колебаний напряжения на конденсаторе будет равна (используем те же обозначения, что и в §20, Механика):
 . (45.7)
. (45.7)
Сдвиг фазы колебаний напряжения на конденсаторе относительно колебаний напряжения источника равен:
 . (45.8)
. (45.8)
При  видно, что
видно, что  , сдвиг фазы стремится к 0. При
, сдвиг фазы стремится к 0. При
резонансе, когда  , для амплитуды установившихся колебаний получим следующее значение:
, для амплитуды установившихся колебаний получим следующее значение:
 .
.
Видим, что при малом затухании отношение амплитуды колебаний при резонансе к амплитуде колебаний напряжения при  равно добротности колебательного контура.
равно добротности колебательного контура.
§42 Сети переменного тока
После внедрения электричества в повседневную жизнь электрические цепи постоянного тока были очень быстро заменены цепями переменного тока. Это связано с простотой преобразования напряжения в сети. Для уменьшения потерь передавать электрическую мощность выгоднее при повышенном напряжении, а использовать электрические цепи с напряжением выше нескольких сотен вольт опасно. Поэтому на электростанции переменное напряжение генератора повышается трансформатором ,передается по сети, а у потребителя понижается также трансформатором до безопасного уровня. В “старом свете” стандартное напряжение в сети имеет амплитудное значение  В и частоту 50 Гц. В “новом свете” напряжение в сети имеет амплитудное значение
В и частоту 50 Гц. В “новом свете” напряжение в сети имеет амплитудное значение  В и частоту 60 Гц.
В и частоту 60 Гц.
Для анализа цепей переменного тока рассмотрим генераторы переменного напряжения, трансформаторы и различные нагрузки. Реальные нагрузки обычно представляют в виде эквивалентной схемы, состоящей из идеальных конденсаторов, индуктивностей и резисторов. Эквивалентные схемы, представляющие какой-то объект, могут существенно различаться в разных частотных диапазонах. Например, хорошо известный Вам соленоид в сети переменного тока частотой 50 Гц может быть заменен эквивалентной схемой из последовательно соединенных идеальных индуктивности и резистора (рис.42.1а). При анализе схемы с такой же индуктивностью на большей частоте может понадобиться учитывать межвитковую емкость, тогда эквивалентная схема может выглядеть так, как показано на рис.42.1b.
Рис.42.1

Генераторы переменного напряжения могут быть различными по конструкции. Один из возможных генераторов очень незначительно отличается от уже рассмотренного нами генератора постоянного тока (рис.39.1). Рамка подключается не к коллекторам в виде полуколец, а к двум изолированным кольцам, напряжение с которых снимается щетками. Напряжение генератора меняется по гармоническому закону с частотой, равной частоте вращения вала:  .
.
Трансформатор представляет собой две катушки, намотанные на одном общем сердечнике с большой магнитной проницаемостью (рис.42.2).
Рис.42.2

Поскольку каждый виток катушки пронизывает одинаковый магнитный поток, то, пренебрегая падением напряжения на активном сопротивлении обмоток, можем утверждать, что  ,
,  , а их отношение равно отношению числа витков в обмотках:
, а их отношение равно отношению числа витков в обмотках:  . Таким образом, используя трансформаторы с разным числом витков в обмотках, мы можем и увеличивать и уменьшать амплитудное значение переменного напряжения в сети.
. Таким образом, используя трансформаторы с разным числом витков в обмотках, мы можем и увеличивать и уменьшать амплитудное значение переменного напряжения в сети.
Основные задачи, которые мы решаем при анализе цепей переменного тока, заключаются в отыскании амплитудных значений тока и напряжения на различных элементах цепи, а также фазовых сдвигов токов и напряжений.
Если подать напряжение  на идеальный резистор, то ток через него по фазе будет совпадать с напряжением:
на идеальный резистор, то ток через него по фазе будет совпадать с напряжением:  . Строго говоря, это утверждение связано с тем, что время релаксации свободных носителей тока должно быть много меньше периода колебаний напряженности поля в проводнике
. Строго говоря, это утверждение связано с тем, что время релаксации свободных носителей тока должно быть много меньше периода колебаний напряженности поля в проводнике  . Конечно, это условие выполняется для цепей переменного тока с частотой 50 Гц.
. Конечно, это условие выполняется для цепей переменного тока с частотой 50 Гц.
При подключении к источнику переменного напряжения идеального конденсатора, напряжение на нем будет равно напряжению источника  . Ток через него найдем дифференцированием по времени заряда конденсатора:
. Ток через него найдем дифференцированием по времени заряда конденсатора:
 .
.
Видим, что ток через конденсатор опережает по фазе напряжение на нем на  . Связь амплитудных значений тока и напряжения позволяет определить емкостное сопротивление:
. Связь амплитудных значений тока и напряжения позволяет определить емкостное сопротивление:
 . (42.1)
. (42.1)
При подключении к источнику переменного напряжения идеальной индуктивности, напряжение на ней будет равно ЭДС индукции:
 , откуда может быть определен ток через индуктивность
, откуда может быть определен ток через индуктивность  . Видим, что ток через индуктивность отстает по фазе от напряжения на ней на
. Видим, что ток через индуктивность отстает по фазе от напряжения на ней на  . Связь амплитудных значений напряжения и тока позволяет определить индуктивное сопротивление:
. Связь амплитудных значений напряжения и тока позволяет определить индуктивное сопротивление:
 . (42.2)
. (42.2)
Если напряжение на каком-либо элементе схемы равно  , а ток через этот элемент сдвинут по фазе на
, а ток через этот элемент сдвинут по фазе на 
 , то средняя мощность, выделяющаяся в нем, будет равна:
, то средняя мощность, выделяющаяся в нем, будет равна:

 . (42.3)
. (42.3)
В идеальной индуктивности и конденсаторе электрическая мощность выделяться не может, поскольку фазовый сдвиг тока относительно напряжения для них равен  .
.
В сопротивлении  будет выделяться мощность
будет выделяться мощность  . Обычно, когда говорят о напряжении в сети переменного тока, то имеют в виду не амплитудное его значение
. Обычно, когда говорят о напряжении в сети переменного тока, то имеют в виду не амплитудное его значение  , а эффективное
, а эффективное  . В этом случае, выделяющаяся в сопротивлении
. В этом случае, выделяющаяся в сопротивлении  мощность
мощность  совпадает с мощностью в сети постоянного тока с таким же напряжением.
совпадает с мощностью в сети постоянного тока с таким же напряжением.
Поскольку при анализе цепей переменного тока одновременно приходится определять и амплитуды и фазы, очень удобным будет использование комплексных чисел. Например, активному сопротивлению  соответствует действительное число
соответствует действительное число  , емкостному сопротивлению соответствует мнимое число
, емкостному сопротивлению соответствует мнимое число  , а индуктивному сопротивлению соответствует мнимое число
, а индуктивному сопротивлению соответствует мнимое число  . Ток в цепи (для примера рассмотрим цепь из последовательно соединенных идеальных резистора, конденсатора и индуктивности) будет также комплексной величиной
. Ток в цепи (для примера рассмотрим цепь из последовательно соединенных идеальных резистора, конденсатора и индуктивности) будет также комплексной величиной  :
:
 .
.
Откуда амплитудное значение силы тока равно:
 .
.
Иногда для анализа цепей переменного тока используют векторные диаграммы, не используя комплексных чисел. С каждым током (или напряжением) связывают вектор, модуль которого равен амплитудному значению тока (напряжения), а направление задается фазовым сдвигом.
Для рассмотренного примера векторная диаграмма напряжений показана на рис.42.3а.
Рис.42.3

Решим задачу о согласовании нагрузки с источником переменного напряжения. В цепи постоянного тока мы для этого могли использовать только последовательное сопротивление  , в котором часть мощности терялась. В цепи переменного тока для согласования мы можем использовать либо емкость, либо индуктивность. В этом случае дополнительных потерь не появится. Пусть у нас есть лампа (или электронагреватель) с активным сопротивлением
, в котором часть мощности терялась. В цепи переменного тока для согласования мы можем использовать либо емкость, либо индуктивность. В этом случае дополнительных потерь не появится. Пусть у нас есть лампа (или электронагреватель) с активным сопротивлением  , рассчитанная на напряжение
, рассчитанная на напряжение  (эффективное), потребляемая мощность
(эффективное), потребляемая мощность  . Нам ее необходимо включить в сеть с переменным напряжением
. Нам ее необходимо включить в сеть с переменным напряжением  , причем напряжение в сети
, причем напряжение в сети  больше напряжения
больше напряжения  . Определим емкость
. Определим емкость  последовательно подключаемого для согласования конденсатора (рис.42.3b). Амплитудное значение силы тока в цепи будет равно:
последовательно подключаемого для согласования конденсатора (рис.42.3b). Амплитудное значение силы тока в цепи будет равно:
 .
.
Падение напряжения на сопротивлении  должно быть равно допустимому напряжению
должно быть равно допустимому напряжению  :
:
 .
.
Искомая емкость будет равна:
 .
.
Сдвиг фазы колебаний тока от фазы колебаний напряжения в цепи будет равен  .
.
Поскольку в наших квартирах используются, в основном, нагрузки с активным сопротивлением, то проблем со сдвигом фаз тока и напряжения не возникает. В промышленности же, если основные потребители электрической энергии – электродвигатели, то может возникнуть значительный сдвиг фазы. Регулирование (уменьшение) сдвига фазы колебаний напряжения и тока в сети – задача, решаемая включением компенсирующих конденсаторов.
В заключение рассмотрим очень важный элемент сетей переменного тока – передающую линию, которая может представлять собой просто два параллельных проводника (воздушные линии электропередач тока промышленной частоты), либо витую пару, либо коаксиальную линию для передачи информации на частотах до ~ 1 Ггц. Важнейшая характеристика подобной линии емкость и индуктивность единицы длины линии  .
.
Рис.42.4

Генератор переменного напряжения  нагружен на передающую линию (для примера, коаксиальный кабель с внутренним проводником радиуса
нагружен на передающую линию (для примера, коаксиальный кабель с внутренним проводником радиуса  и внешним цилиндрическим заземленным проводником радиуса
и внешним цилиндрическим заземленным проводником радиуса  ) бесконечной длины (рис.42.4а). Пусть
) бесконечной длины (рис.42.4а). Пусть  и
и  - индуктивность и емкость единицы длины кабеля. Мы их уже определили (выражения 20.5 и 8.3).
- индуктивность и емкость единицы длины кабеля. Мы их уже определили (выражения 20.5 и 8.3).
Сопротивление  такого кабеля, подключенного к генератору, мы можем определить следующим образом. Мысленно выделим начальный кусок кабеля длиной
такого кабеля, подключенного к генератору, мы можем определить следующим образом. Мысленно выделим начальный кусок кабеля длиной  . На эквивалентной схеме цепь, подключенная к генератору, будет выглядеть так, как показано на рис. рис.42.4b. Для общего сопротивления последовательно соединенных индуктивности и цепи из конденсатора и
. На эквивалентной схеме цепь, подключенная к генератору, будет выглядеть так, как показано на рис. рис.42.4b. Для общего сопротивления последовательно соединенных индуктивности и цепи из конденсатора и  получим уравнение:
получим уравнение:
 .
.
Решая его и избавляясь от мнимой единицы в знаменателе, получим:
 .
.
Предел этого выражения при 

даст нам активное сопротивление, которое называют волновым сопротивлением кабеля. Реактивное сопротивление стремится к нулю, поэтому колебания тока и напряжения в линии будут совпадать по фазе.
Падение напряжения на участке длиной  будет равно:
будет равно:
 .
.
Переходя к пределу, получим уравнение:
 .
.
Заряд кабеля на участке  равен
равен  . Его изменение
. Его изменение  , обусловленное разностью токов
, обусловленное разностью токов  , после перехода к пределу равно:
, после перехода к пределу равно:
 .
.
Получили еще одно уравнение:
 .
.
Исключая из этих двух уравнений, например, ток (дифференцируя первое по  , второе по
, второе по  ), получим уравнение:
), получим уравнение:
 .
.
Или, если теперь вернуться в Гауссову систему, то уравнение будет выглядеть так:
 .
.
Это хорошо известное нам волновое уравнение, которое описывает волну, бегущую вдоль оси  :
:  . Фазовая скорость волны
. Фазовая скорость волны  определяется из множителя в правой части уравнения:
определяется из множителя в правой части уравнения:
 . (42.4)
. (42.4)
Подставляя значения  и
и  , получим фазовую скорость волны в кабеле с вакуумным зазором, равную скорости света с. Если зазор будет заполнен диэлектриком с относительной диэлектрической проницаемостью
, получим фазовую скорость волны в кабеле с вакуумным зазором, равную скорости света с. Если зазор будет заполнен диэлектриком с относительной диэлектрической проницаемостью 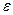 и магнитной проницаемостью
и магнитной проницаемостью  , то фазовая скорость будет равна
, то фазовая скорость будет равна
 .
.
Мы решили задачу для бесконечно длинного кабеля. Если на другом конце кабеля не будет возникать отраженной волны, то наше решение будет справедливо и для кабеля конечной длины. Для того, чтобы на противоположном конце кабеля не возникало отраженной волны, его надо нагрузить на активное сопротивление, равное волновому сопротивлению кабеля (согласованная нагрузка).