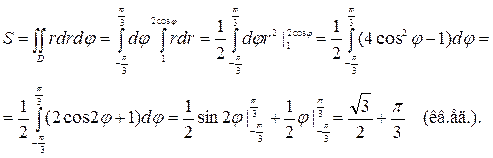Вычисление площадей плоских фигур, ограниченных замкнутыми линиями

 

Формулы для вычисления площадей плоских фигур с помощью двойного интеграла имеют вид:

1) в декартовой системе координат ;

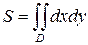2) в полярной системе координат .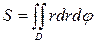

Пример 4.1. Найти площадь области D, ограниченной эллипсом .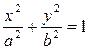

Решение 1. Так как эллипс симметричен относительно начала и осей координат, то S_фиг = 4S₁, где S₁ –– четверть эллипса, лежащая в первой четверти (см. рис. 7). Для этой части эллипса x изменяется от 0 до a, y от 0 до .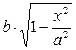

2. (кв. ед.).

Последний интеграл вычислили с помощью подстановки x = asint, где .

Пример 4.2. Найти площадь части круга x² + y² 2x, содержащейся вне окружности x² + y² = 1.

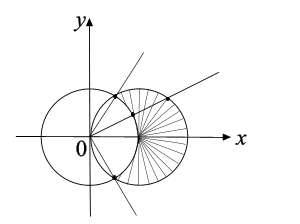
Решение. Изобразим данную область на координатной плоскости (рис. 8).

Так как уравнения линий, ограничивающих область интегрирования содержат сумму (x² + y²), то для вычисления интеграла выгодно перейти к полярной системе координат:

a) x² + y² = 1 → r = 1;

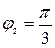
б) x² + y² = 2x → r = 2cos .

Чтобы найти пределы изменения полярного угла , найдем координаты точек пересечения окружностей. Решая совместно уравнения r = 1 и r = 2cos , получаем 1 = 2cos или .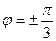

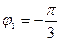
Рис. 8

Итак,