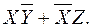Диаграммы Венна
Логические функции можно отобразить на диаграммах Венна. Пусть левый круг (рис. 3.5) соответствует области прямых

значений переменной А, правый — области прямых значений переменной В. Тогда область, образующаяся при пересечении кругов, соответствует логическому произведению АВ. Область, образующаяся при наложении кругов, соответствует логической сумме А + В. Часть круга А, куда не входит В, соответствует логическому произведению  . Операции неравнозначности соответствует область, занимаемая двумя сегментами:
. Операции неравнозначности соответствует область, занимаемая двумя сегментами:  и
и  .
.
С помощью диаграмм Венна легко доказывается справедливость логических тождеств. Для этого надо убедиться, что левой и правой частям записанных логических выражений соответствует одинаковое отображение на диаграмме Венна. Так, при наложении круга А и сегмента АВ мы сохраняем отображение круга А, т. е. А+АВ = А. При наложении отображения A Å B и сегмента АВ получаем отображение логической суммы А + В, т. е. A Å B + АВ = А+В. Если в области А+В исключить сегмент АВ, то получим отображение операции «Исключающее ИЛИ», т. е. 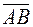 (А+В) = A Å B.
(А+В) = A Å B.
Для доказательства тождества 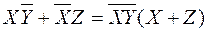 удобно воспользоваться диаграммой Венна для логической функции трех переменных. Если в области X+Z исключить сегмент XY, получим отображение правой части выражения. Оно совпадает с отображением левой части, получаемым путем наложения сегментов
удобно воспользоваться диаграммой Венна для логической функции трех переменных. Если в области X+Z исключить сегмент XY, получим отображение правой части выражения. Оно совпадает с отображением левой части, получаемым путем наложения сегментов