В прошивных станах Маннесмана, Штифеля и Дишера

Для определения усилий, возникающих при прокатив, необходимо сначала найти площадь соприкосновения металла с валками, что для прошивных станов уже сделано выше.

Считая выводы Грубера [82] по определению площади соприкос­новения металла с валками не лишенными погрешностей, Целиков [64] вместо формул (76) и (77) для подсчета В 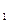и В применяет лишь одну формулу:

(188)

где — диаметр валка в сечении х—х;

—диаметр гильзы в том же сечении х—х;

— уменьшение толщины заготовки за половину оборота по­следней.

Подставляя численные значения и сравнивая полученные результа­ты по указанным формулам, приходим к выводу, что для станов Маннесмана формула Целикова (188) по сравнению с формулами Грубе­ра (76) и (77) дает увеличение лишь на 0,5 1%.

По стану Штифеля Целиков дает для различных поясов деформа­ции формулу:

(189)

где — диаметр гильзы в сечении первого пояса.

Такая же формула дается для второго пояса деформации, где вме­сто необходимо брать .

Сравнивая формулу (189) с формулами Грубера (76) и (77), ви­дим, что формула Целикова дает результаты, преувеличенные при­мерно на 10—12%.

Рассматривая силы, действующие на валки при поперечной про­катке аналогично силам, действующим на обкатывающие плиты (фиг. 113, а), мы, отождествляя их, придем к выводу, что силы Р, Р, действующие на плиты или валки, равны и направлены в противопо­ложные стороны, так как на материал никакие другие силы не дей­ствуют, и кроме того при равномерном движении материала геометри­ческая сумма этих сил равна нулю.

Из фиг. 113, б видно, что равнодействующая общего давления Р, приложенная в точке, соответствующей , проходит через центр, имея плечо, равное а.

Зная величины составляющих силы Р, спроектированной на гори­зонтальную и вертикальную плоскости:

(190)

(191)

 

и угол , можно определить момент, необходимый для привода валка (без учета сил трения в подшипниках):

или

(192)

Тогда мощность (также без учета трения в подшипниках) будет:

(193)

где — скорость движения материала.

Прежде чем перейти к определению направления усилий, действующих на диски в прошивном стане Штифеля, рассмотрим силы, действующие на заготовку и оправку.

При равномерном движении заготовки и равномерном вращении оправки и при отсутствии внешних сил, геометрическая сумма усилий, действующих на всю систему, равна нулю.

На фиг. 114, а показана схема сил, действующих на заготовку в прошивном стане Штифеля, причем приложение этих сил выбрано произвольно в точке А вблизи центра тяжести площади соприкосновения заготовки с дисками, а элементарные силы каждого из них сведены к двум равнодействующим Р и Т, первая из которых направлена перпендикулярно к оси заготовки, вторая параллельно ее оси. Действие упорного подшипника представлено силой , направленной в сторону, расположенную направлению движения заготовки.

Составляя уравнение равновесия сил, действующих на заготовку с оправкой, спроектируем их на ось заготовки:

(194)

откуда

 

 

Фиг. 11З. Силы, действующие при поперечной прокатке: а — на плиты; б — на валки

 

Уравнение (194) показывает, что действующие со стороны валков на заготовку касательные силы Т и со стороны упорного подшипника сила направлены в противоположные стороны.

Так как по условиям равновесия сумма моментов всех сил, дей­ствующих на заготовку с оправкой относительно оси заготовки, должна равняться нулю, то силы Р, действующие со стороны дисков, должны проходить через ось заготовки.

Действие со стороны заготовки на диски представлено теми же силами Р и Т, но направленными в противоположную сторону (фиг. 114,б).

Раскладывая по трем взаимно-перпендикулярным направлениям силы Р и Т, действующие на диски, получаем горизонтальное давле­ние, действующее на эти диски и направленное перпендикулярно к их вертикальным осям.

На первый диск:

или

(195)

На второй диск:

или

(196)

Здесь — угол между силой Р и горизонтальной плоскостью, причем этот угол можно определить из уравнения:

(197)

где а—расстояние от точки приложения равнодействующей давления диска на заготовку до плоскости прокатки;

—радиус сечения заготовки, в котором приложена равнодействующая сила.

Вертикальное давление на оба диска одинаково:

или

(198)

Осевое давление на первый диск:

(199)

На второй диск:

(200)

Определив давление по всем трем направлениям, можно подсчи­тать момент, необходимый для вращения дисков.

Для вращения первого диска (без учета сил трения в подшипниках) этот момент будет:

или согласно уравнениям (198) и (195) М 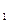будет:

(201)

Для вращения второго диска момент будет:

или согласно уравнениям (198) и 196) М будет:

(202)

Уравнения (201 и 202) показывают, что для вращения первого диска, расположенного со стороны входа шатуна, требуется момент больший, чем для вращения другого диска, расположенного со сторо­ны упора оправки.

Отсутствие экспериментальных данных по определению удельного давления на валках прошивных станов вынуждает пользоваться под­счетом последнего по методу, который аналогичен принятому для сор­товых станов.

Подсчитав общее давление по формулам Экелунда (31) и (35), где вместо толщины полосы и следует брать толщину стенки трубы перед обжатием и после обжатия , и зная площадь соприкоснове­ния металла с валками в обоих поясах деформации (81) и (189), можно определить удельное давление р.

Зная удельное давление и площадь соприкосновения диска с заго­товкой во втором поясе деформации, можно также определить силу , действующую на оправку в осевом направлении.

Во втором поясе деформации давление дисков на заготовку пол­ностью передается и на оправку (фиг. 114, в), причем оно приложено к поверхности оправки только на участках и , где происходит уменьшение толщины заготовки; на остальной поверхности оправка не испытывает давления.

Считая, что оправка состоит из двух рабочих конических поверх­ностей (фиг. 114, в) с углами наклона этих поверхностей к оси оправки и определяем давление дисков 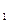Р и Р на заготовку от­дельно для первого и второго участков.

Обозначая коэффициент трения через ,находим:

(203)

Подобным же образом можно определить силу для оправки лю­бой формы, приравнивая кривую образующей оправки к ломаной ли­нии, т. е., рассматривая оправку, как состоящую из целого ряда кони­ческих поверхностей.

В прошивном стане Маннесмана (фиг. 115, а, б, в), раскладывая силы Р и Т как указано выше для станов Штифеля по трем взаимно перпендикулярным направлениям, получаем давление на валок по оси X (фиг. 115, а).

(204 а)

или

(204 б)

 

Фиг. 114, а и б. Схема действия сил в прошивном стане; а — на заготовку;

б — на диски

Фиг. 114, в. Схема действия сил в прошивном стане на оправку

Фиг. 115. Схема сил, действующих на валки в стане Маннесмана: а — поперечный разрез по валкам; б — вид сверху на валки; в — про­дольный разрез по заготовке

 

Угол определяется из уравнения:

где а — расстояние от точки приложения равнодействующей давления валка на заготовку до прямой, соединяющей оси валков с осью заготовки в плоскости действия силы Р;

—радиус заготовки в сечении, где приложена сила Р.

Согласно фиг. 115, б давление на валок, направленное по оси , равняется:

или

(205)

Давление в направлении оси валка равняется:

или

(206)

Без учета сил трения, момент, необходимый для вращения каждого валка,

(207)

где — радиус валка в плоскости равнодействующей давления.

Подставляя в это уравнение значения сил X и из уравнений (204) и (205), получаем:

(208)

Подсчет сил Р и Т можно вести по методу, принятому для диско­вых прошивных станов.

При определении величины и направления сил, действующих на валки в прошивных станах Дишера и Штифеля с бочкообразными вал­ками, можно пользоваться изложенным выше методом.