В станах Краузе
Стан системы Краузе существенно отличается от станов, рассмотренных выше, по характеру процесса деформации, конструкции рабочей клети и особенностям устройства рабочей линии стана.
В стане Краузе имеется подвижная станина, которая приводит во вращение валки, накатывающиеся на полосу благодаря трению их о внутренние плоскости станины. Прежде чем перейти к разбору взаимодействия сил в этом стане рассмотрим несколько случаев распределения сил при равномерно катящихся под действием внешних усилий тяжелых цилиндров.
Если цилиндр катится без скольжения (1-й случай) и нормальное давление равно N (фиг. 105, а), то для обеспечения вращения цилиндра необходимо преодолеть действие пары сил, момент которой
 (150)
(150)
где  —коэффициент трения качения, измеряемый в сантиметрах.
—коэффициент трения качения, измеряемый в сантиметрах.
Условие равновесия сил для этого случая представляется уравнением:
 (151)
(151)
где  — алгебраическая сумма моментов, действующих на цилиндр;
— алгебраическая сумма моментов, действующих на цилиндр;
 — приводная сила;
— приводная сила;
 —диаметр цилиндра.
—диаметр цилиндра.
Из уравнения (151) определяем:
 (152)
(152)

Фиг. 105. Распределение сил при качении тяжелых цилиндров: а — по одной плоскости; б — между двумя параллельными плоскостями; в — между параллельными плоскостями, наклоненными к горизонтали под углом 
В случае нагрузки, показанной на фиг. 105,б (2-й случай), величина момента М  определяется из уравнения:
определяется из уравнения:

а приводная сила
 (153)
(153)
При наклонных плоскостях (3-й случай) условия (фиг. 105, в) по сравнению с первыми двумя случаями изменяются и точка приложения силы N перемещается из В в В 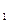 на расстоянии ВВ
на расстоянии ВВ 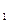 . От вертикальной плоскости, проходящей через центр цилиндра, точка В
. От вертикальной плоскости, проходящей через центр цилиндра, точка В 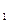 отстоит на расстоянии АВ
отстоит на расстоянии АВ 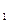 =е, где
=е, где
е = с + f. Таким образом при направляющих плоскостях, имеющих наклон к горизонтали под углом  направление силы N перпендикулярно к этим плоскостям и проходит также под углом
направление силы N перпендикулярно к этим плоскостям и проходит также под углом  , но уже к вертикали, а величина момента М
, но уже к вертикали, а величина момента М  и силы
и силы  определяется из уравнения:
определяется из уравнения:

отсюда приводная сила:
 (154)
(154)
Сравнивая уравнения (152), (153) и (154), приходим к выводу, что во всех трех случаях приводная сила  имеет разную величину несмотря на то, что прилагается одинаковое давление N. Во втором случае она вдвое больше, чем в первом, в третьем — больше, чем во тором на величину, определяемую наклоном плоскостей, вызывающим увеличение плеча пары сил или изменение угла наклона .
имеет разную величину несмотря на то, что прилагается одинаковое давление N. Во втором случае она вдвое больше, чем в первом, в третьем — больше, чем во тором на величину, определяемую наклоном плоскостей, вызывающим увеличение плеча пары сил или изменение угла наклона .
Однако и третий из разобранных случаев не дает полной аналоги со случаем распределения сил на валках стана Краузе, а дает лишь некоторое приближение к нему.
Рассматривая взаимодействие сил между полосой и валками, заключенными в станину клети с направляющими наклонными плоскостями (фиг. 106), представим себе верхний валок в виде цилиндра,
равномерно катящегося под действием силы  приложенной в точке В'. Накатываясь на полосу валки (цилиндры), защемленные между наклонными плоскостями, деформируют полосу, имеющую конусообразное сечение в направлении прокатки.
приложенной в точке В'. Накатываясь на полосу валки (цилиндры), защемленные между наклонными плоскостями, деформируют полосу, имеющую конусообразное сечение в направлении прокатки.
Наличие сопротивления трения качения в наклонных плоскостях станины вызывает перемещение точки приложение равнодействующей элементарных давлений R, направленной по радиусу ОС из С в С  ,на величину плеча 2
,на величину плеча 2  (фиг. 106).
(фиг. 106).

Фиг. 106. Схема взаимодействия сил в стане системы Краузе
В свою очередь давление валка на металл вызывает силы трения, равнодействующая которых Т проходит по касательной к валку в направлении его движения.
Равнодействующая общего давления Р валка на металл определяется из слагающих 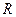 и Т. Она располагается параллельно плоскости, перпендикулярной к наклонным плоскостям станины и проходящей через ось валка.
и Т. Она располагается параллельно плоскости, перпендикулярной к наклонным плоскостям станины и проходящей через ось валка.
Таким образом на валок действует система сил, препятствующих его перемещению. К ним необходимо отнести: силы сопротивления трения качения валка в наклонных плоскостях (принимая при этом полосу за вторую плоскость) и силы сопротивления, вызываемые деформацией полосы. Все эти силы можно свести к паре сил, равных по величине равнодействующей Р с плечом
 (155)
(155)
где а — плечо равнодействующей сил, вызываемых деформацией полосы и равное половине проекции дуги захвата

 — плечо сил сопротивления трения качения.
— плечо сил сопротивления трения качения.
Отсюда момент сил, сопротивляющихся перемещению валка, в том числе сил сопротивления трения качения и сил, вызываемых деформацией:
 (156)
(156)
Момент сопротивления перемещению валков (156) может преодолеваться моментом приводной силы  , приложенной к точке В с плечом, равным диаметру валка
, приложенной к точке В с плечом, равным диаметру валка  , взятым относительно оси В'. Действие сил этого момента (приводного) можно свести также к паре сил, если к точке В приложить в одном направлении фиктивную силу
, взятым относительно оси В'. Действие сил этого момента (приводного) можно свести также к паре сил, если к точке В приложить в одном направлении фиктивную силу  (показана пунктиром), сопротивляющуюся перемещению валка и равную и противоположную по направлению силе
(показана пунктиром), сопротивляющуюся перемещению валка и равную и противоположную по направлению силе  ,приложенной в точке В для ее уравновешивания.
,приложенной в точке В для ее уравновешивания.
На основании сказанного, определив приводной момент, можно составить уравнение для суммы моментов, действующих на систему:
 (157)
(157)
откуда

а сила, приложенная к станине для преодоления сопротивления деформации, вызываемой верхним валком, и сил сопротивления трения качения между плоскостями:
 (158)
(158)
где  — угол наклона плоскости станины.
— угол наклона плоскости станины.
Обозначая силу тяги станины или давления шатуна через  , силу сопротивления трения в шейках валков и направляющих клети через
, силу сопротивления трения в шейках валков и направляющих клети через  можем написать уравнение равновесия сил:
можем написать уравнение равновесия сил:
 (159)
(159)
Из уравнения (159) видно, что сила тяги  равна сумме проекций слагающих равнодействующей общего давления
равна сумме проекций слагающих равнодействующей общего давления  , и сумме сил
, и сумме сил  , где
, где  —сопротивление трения в обойме валков,
—сопротивление трения в обойме валков,  —сопротивление в направляющих станины. В свою очередь
—сопротивление в направляющих станины. В свою очередь  , где
, где  — коэффициент трения в обойме на шейках валков с роликовыми подшипниками,
— коэффициент трения в обойме на шейках валков с роликовыми подшипниками,

где  — вес станины,
— вес станины,
 — коэффициент трения скольжения на направляющих станины.
— коэффициент трения скольжения на направляющих станины.
Коэффициенты трения качения в условиях практики можно принимать равными: для роликовых подшипников  =0,0015
=0,0015  0,0035, для стальных направляющих и стальных валков в среднем
0,0035, для стальных направляющих и стальных валков в среднем  = 0,05
= 0,05  0,15.
0,15.
Из уравнений (158) и (159) сила тяги  (без учета сопротивления рейке) определяется в зависимости от общего давления Р и величины плеча
(без учета сопротивления рейке) определяется в зависимости от общего давления Р и величины плеча  :
:
 (160)
(160)
Введя вместо  его значение из формулы (158), получаем:
его значение из формулы (158), получаем:
 (161)
(161)
Величину плеча а равнодействующей общего давления металла на валки Р для учета наклона плоскости и сопротивления трения можем определить по формуле (93):

где  —угол конусности полосы.
—угол конусности полосы.
Но так как точка приложения равнодействующей общего давления переместилась из С в С  , то плечо фактически увеличилось на величину
, то плечо фактически увеличилось на величину  , что обусловлено наличием трения сопротивления в плоскостях станины (для одного валка — между плоскостью станины и прокатываемым материалом) и действительную величину плеча можно выразить так:
, что обусловлено наличием трения сопротивления в плоскостях станины (для одного валка — между плоскостью станины и прокатываемым материалом) и действительную величину плеча можно выразить так:
 (162)
(162)
Угол  примерно равен 14—15°.
примерно равен 14—15°.
Коэффициент трения между стальными направляющими и стальным валком принимаем  =0,1 см.
=0,1 см.
Угол наклона плоскостей  =4—5°.
=4—5°.
Радиус валка  = 125 мм.
= 125 мм.
Тогда уравнение (162) принимает следующее числовое выражение:

При этом нужно учесть еще поворот равнодействующей на угол  , равный углу наклона направляющих — 3—6°;
, равный углу наклона направляющих — 3—6°;  3° соответствует длине плеча, равной около 6 мм. Этот поворот оказывает влияние не на величину плеча, а на перемещение точки приложения равнодействующей (при
3° соответствует длине плеча, равной около 6 мм. Этот поворот оказывает влияние не на величину плеча, а на перемещение точки приложения равнодействующей (при  равнодействующая Р занимает вертикальное положение); эта точка удаляется от линии центров валка примерно на:
равнодействующая Р занимает вертикальное положение); эта точка удаляется от линии центров валка примерно на:

длины дуги захвата.
На основании уравнения (161) с учетом потерь в шатуне, кривошипе и других частях привода стана (величина потерь определяется коэффициентом  ) можно найти усилие на кривошипе
) можно найти усилие на кривошипе

Задавшись радиусом кривошипа 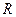 , определяем вращающий момент привода кривошипа
, определяем вращающий момент привода кривошипа

При обеспечении условий для осуществления процесса прокатки на стане необходимо, чтобы
 (163)
(163)
Задавшись радиусом 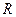 и зная
и зная  —значение коэффициента полезного действия стана, можно легко определить приводной момент, а также мощность на приводном валу.
—значение коэффициента полезного действия стана, можно легко определить приводной момент, а также мощность на приводном валу.
Принимая во внимание потери на приводном валу и в муфте  , можно определить мощность мотора стана, если мотор одновременно не обслуживает другие вспомогательные операции.
, можно определить мощность мотора стана, если мотор одновременно не обслуживает другие вспомогательные операции.