Вынужденные вертикальные колебания судна
Если на судно действует периодическая внешняя сила, связанная с морской волной, то последнее начинает совершать вынужденные колебания в вертикальном направлении. Рассмотрим основные закономерности этих колебаний.
Уравнение морской волны имеет вид
 . .
| (21.55) |
Обозначим через z=z(t) смещение центра тяжести судна относительно невозмущенной поверхности моря. В отсутствии морской волны на судно действовала сила Архимеда FA = –gSz. При появлении волны происходит дополнительное вертикальное смещение на величину x и сила Архимеда
 .
.
Кроме силы Архимеда, следует учесть силу сопротивления:
 .
.
Использовав второй закон Ньютона, получим уравнение колебаний

или
 .
.
Подставим в последнее выражение x и 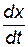 из (21.55). В результате получим дифференциальное уравнение вынужденных колебаний судна:
из (21.55). В результате получим дифференциальное уравнение вынужденных колебаний судна:
 . .
| (21.56) |
где w0 — частота собственных колебаний судна (см. § 21.5).
Из сопоставления (21.55) и (21.47) находим
 . .
| (21.57) |
В данном случае величина F0/m — комплексная. Поскольку физический смысл имеет модуль комплексной величины F0/m, умножим (21.57) на величину комплексно-сопряженную, т.е. на  и извлечем квадратный корень:
и извлечем квадратный корень:
 ;
;
 . .
| (21.58) |
Подставив (21.58) в выражение для амплитуды вынужденных колебаний (21.50), получим:
 . .
| (21.59) |
Из (21.59) видно, что амплитуда вынужденных колебаний судна зависит от частоты w морской волны. Можно показать, что резонанс наступает, когда частота волн
 .
.
Для того, чтобы избежать резонансных колебаний судна, на стадии его проектирования нужно предусмотреть, чтобы резонансная частота возможно более отличалась от частот w морских волн, характерных в штормовую погоду. Если же судно все-таки попало в область резонанса, то следует изменить скорость или направление движения судна, чтобы изменить частоту ударов набегающих волн.