Сложение взаимно перпендикулярных (векторных) колебаний
Пусть материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях одинаковой частоты, описываемых уравнениями
 , ,
| (21.28) |
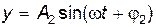 , ,
| (21.29) |
Для нахождения траектории результирующего движения исключим из уравнений (21.28) и (21.29) время t. Для этого преобразуем эти уравнения к виду:
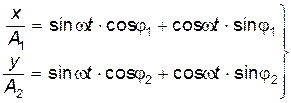
|
Получили линейную систему уравнений относительно sin wt и cos wt, решая которую, находим
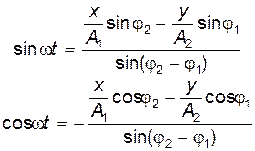
|
Подставим полученные значения sin wt и cos wt в тождество sin 2wt+cos 2wt = 1. После несложных преобразований получим
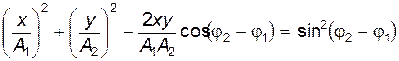 . .
| (21.30) |
Последнее уравнение представляет собой обобщенное уравнение эллипса.
Рассмотрим теперь несколько частных случаев.
1. Разность фаз складываемых колебаний равна нулю, т.е. j2 – j2 = 0. Тогда из (21.30) следует
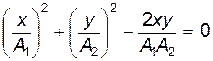 . .
|
Из полученного выражения видно, что в этом случае траектория движения материальной точки представляет собой прямую
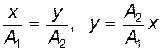 , ,
|
проходящую через первый и третий квадранты (рис. 21.10, а).
2. Разность фаз j1 - j2 = p. Из (21.30) следует
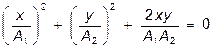 , ,
|
т.е. в этом случае траектория тоже прямолинейна
 , ,
|
но проходит через второй и четвертый квадранты (рис. 21.10, б).
3. Разность фаз  . Тогда движение будет происходить по эллиптической траектории (рис. 21.10, в)
. Тогда движение будет происходить по эллиптической траектории (рис. 21.10, в)
 , ,
|
отнесенной к осям координат. По такой же траектории будет двигаться точка, если  , однако в этом случае вращение будет проходить против часовой стрелки.
, однако в этом случае вращение будет проходить против часовой стрелки.
В частном случае, если A1 = A2, движение будет проходить по окружности.

Рис. 21.10
При любых других значениях разности фаз траекторией движения будет эллипс, не приведенный к осям координат (рис. 21.10, г).
Более сложные криволинейные траектории получаются при сложении взаимно перпендикулярных колебаний различной частоты. В тех случаях, когда отношение частот выражается рациональным числом, траектории представляют собой замкнутую кривую, называемую фигурой Лиссажу, в других же случаях кривая будет незамкнутой.
Фигуры Лиссажу находят применение для определения частоты и формы складываемых колебаний. Исследование формы колебаний основано на том, что наш глаз четко улавливает малейшие отклонения от прямой или эллипса, которые вызываются тем, что складываемые колебаний не имеют строго синусоидальной формы.