Дифференциальное уравнение гармонических колебаний

Исходя из (21.1), можно получить выражения для скорости v и ускорения a в гармоническом движении:

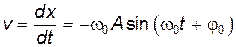;	(21.4)
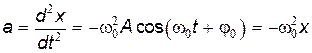.	(21.5)

Используя комплексную форму гармонического колебания (21.3), можно получить эквивалентные выражения для скорости и ускорения:

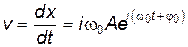;	(21.4а)
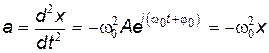.	(21.5а)

Если воспользоваться формулой Эйлера (см. математическую справку) и взять действительную часть выражений (21.4а) и (21.5а), то получим (21.4) и (21.5).

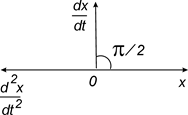Рис. 21.2

Если начало отсчета времени выбрать так, чтобы 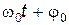, то

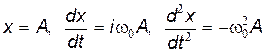. На комплексной плоскости числа 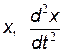расположатся на действительной оси, а число 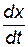— на мнимой (рис. 21.2). Видно, что разность фаз между скоростью 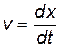и смещением x равна p/2. Ускорение 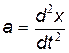и смещение x колеблются в противофазе.

Из (21.5) следует уравнение гармонических колебаний в дифференциальной форме:

.

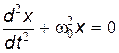(21.6)