Напряжение в наклонных сечениях при растяжении или сжатии

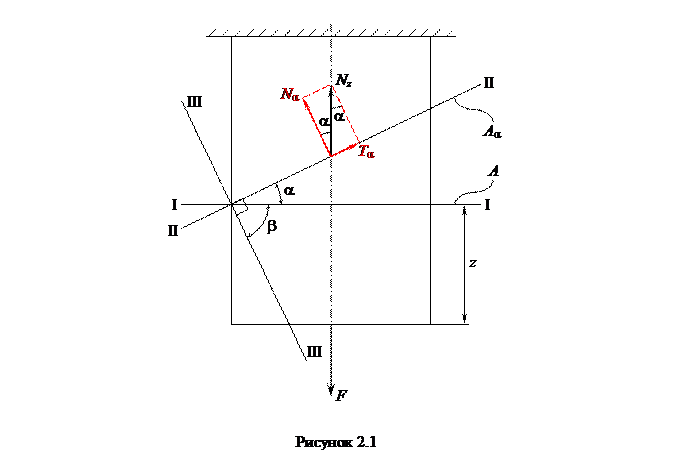
Выделим в растянутом стержне два сечения – поперечное (I–I) с площадью A и наклонное (II–II) с площадью A_a (рисунок 2.1).

В наклонном сечении (II–II) возникает продольная сила N_z, которую удобно разбить на две составляющие – нормальную N_a и касательную T_a к сечению (II–II).

В наклонном сечении возникают нормальные и касательные напряжения, определяемые следующим образом:

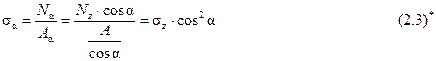
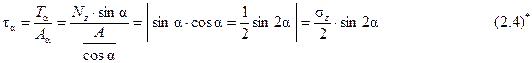
Анализируя зависимости (2.3) и (2.4), выясним при каких углах s и t будут максимальны.

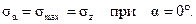
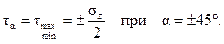
Полученное условие позволяет объяснить характер разрушения многих элементов конструкций по схеме нормального отрыва или по схеме касательного сдвига, или смещения (рисунок 2.2).

Проведем еще одно касательное сечение (III–III) под углом b к сечению (I–I) или перпендикулярно к сечению (II–II).

Определим напряжения, действующие в сечении (III–III), для чего воспользуемся зависимостями (2.3), (2.4) и (2.5).

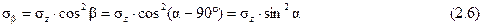
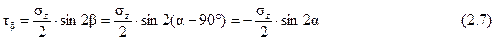
Сложим нормальные и касательные напряжения, действующие в сечениях (II–II) и (III–III):

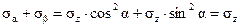
(2.8)*

Зависимость (2.8) выражает закон суммы нормальных напряжений: сумма нормальных напряжений, действующих на двух взаимно перпендикулярных площадках есть величина постоянная и равная максимальному нормальному напряжению, возникающему в поперечных сечениях растянутого стержня.

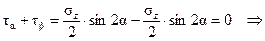
Þ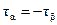

(2.9)*

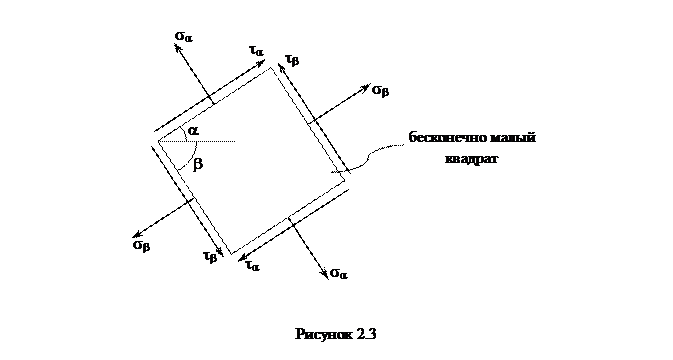
Зависимость (2.9) выражает закон парности касательных напряжений: касательные напряжения, действующие на двух взаимно перпендикулярных площадках равных по величине и противоположных по направлению (рисунок 2.3).