Исследование нелинейных систем методом фазовой плоскости
Цель работы: исследовать поведение нелинейной системы и влияние нелинейных элементов на фазовые траектории.
Общие положения
Метод фазовой плоскости (ФП) используется для исследования динамики и устойчивости систем второго порядка как линейных, так нелинейных с любым типом нелинейного элемента. Фазовая траектория (ФТ) – движение изображающей точки на плоскости с координатами: ось Х – выходная координата системы, ось У – скорость изменения выходной координаты 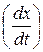 . Совокупность ФТ для различных начальных условий и особых точек (точек равновесия) называют фазовым портретом системы. Он дает возможность оценить поведение системы и устойчивость «в большом», «в малом» и в целом.
. Совокупность ФТ для различных начальных условий и особых точек (точек равновесия) называют фазовым портретом системы. Он дает возможность оценить поведение системы и устойчивость «в большом», «в малом» и в целом.
Уравнения ФТ получают из системы уравнений первого порядка, разрешенных относительно первых производных:
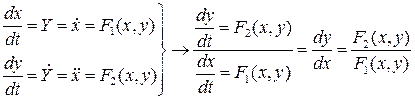
 (*)
(*)
Интегрируя (*), получают уравнение ФТ:
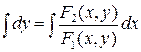
Для устойчивой системы ФТ представляют собой закручивающиеся логарифмические спирали; если в системе возникают незатухающие колебания, то ФТ, соответствующая этому режиму, замкнута (предельный цикл); если колебания расходятся, то логарифмическая спираль раскручивается. Если система содержит нелинейные элементы (НЭ) с кусочно-линейными статическими характеристиками, то фазовая плоскость разбивается линиями переключения, проходящими через точки излома НЭ, на области с различными уравнениями ФТ, их смена проходит на линии переключения.
При исследовании свободного движения необходимо задать начальное положение изображающей точки (  ), при устойчивой системе ФТ стремится:
), при устойчивой системе ФТ стремится:
а) к началу координат ( 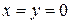 ) или зоне нечувствительности (при наличии соответствующего НЭ);
) или зоне нечувствительности (при наличии соответствующего НЭ);
б) предельному циклу – если возникает режим незатухающих автоколебаний.
При исследовании вынужденного движения 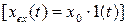 начальное положение изображающей точки может быть любое, а ФТ заканчивается в точке с координатами
начальное положение изображающей точки может быть любое, а ФТ заканчивается в точке с координатами  ,
, 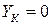 ; где
; где  – некоторое отклонение, обусловленное наличием зоны нечувствительности. При наличии незатухающих колебаний – ФТ – предельный цикл, смещенный на координату
– некоторое отклонение, обусловленное наличием зоны нечувствительности. При наличии незатухающих колебаний – ФТ – предельный цикл, смещенный на координату 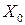 .
.
Порядок выполнения лабораторной работы
1. Собрать систему, показанную на рисунке 1 (линейная часть системы астатическая).
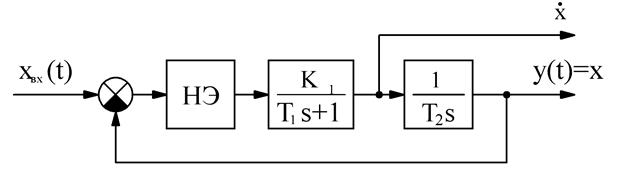
Рисунок 1 – Структура системы
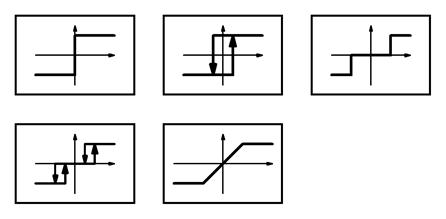
Рисунок 2 – Виды нелинейных элементов
2. Задать НЭ и его параметры и параметры линейной части (  ).
).
3. Задать начальное положение изображающей точки.
4. Снять графики 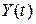 ,
, 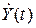 и ФТ.
и ФТ.
5. Пункты 3 и 4 повторить для различных НЭ, изменив зону нечувствительности и неоднозначности, коэффициент усиления.
6. Исследовать вынужденное движение для релейных систем, задав 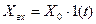 ,
, 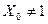 .
.
7. Сделать выводы о влиянии НЭ на поведение системы.
8. Собрать схему на рисунке 3 (система статическая)
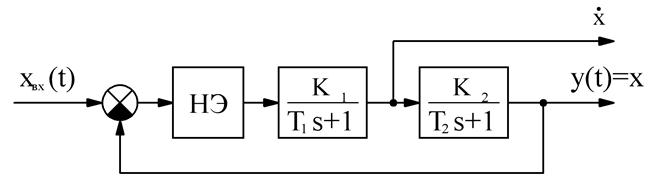
Рисунок 3 – Структура системы
Повторить исследования по пунктам 2-7.
Содержание отчета
1. Схемы исследования.
2. Результаты исследования (ФТ и графики изменения во времени выходной координаты и скорости).
3. Нанести на ФТ линии переключения. Оценить:
а) влияние зон нечувствительности и неоднозначности и коэффициента усиления линейной части на поведение системы;
б) влияние астатизма;
в) сделать выводы об устойчивости системы.
4. Записать уравнения ФТ.