Магнитное поле движущегося заряда. Направление вектора магнитной индукции

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1]; магнитная составляющаяэлектромагнитного поля^[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.

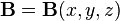Основной силовой характеристикой магнитного поля является вектор магнитной индукции (вектор индукции магнитного поля)^[3][4]. С математической точки зрения — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

· Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции а вектор напряжённости магнитного поля 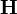, что формально можно сделать, так как в вакууме эти два вектора совпадают^[5]; однако в магнитной среде вектор 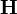не несет уже того же физического смысла^[6], являясь важной, но всё же вспомогательной величиной. Поэтому при формальной эквивалентности обоих подходов для вакуума, с систематической точки зрения следует считать основной характеристикой магнитного поля именно

Магнитное поле можно назвать особым видом материи^[7], посредством которого осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.

Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей.

Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются, в частности, свет и все другие электромагнитные волны.

 

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правогобазиса^[1] в трехмерном пространстве, соглашения о положительной ориентации базиса в нём, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

В частности, это относится к определению направления^[2] таких важных в физике аксиальных векторов, как вектор угловой скорости, характеризующий скорость вращения тела, вектор магнитной индукции B и многих других, а также для определения направления таких векторов, которые определяются через аксиальные, например, направление индукционного тока при заданном векторе магнитной индукции.

· Для многих из этих случаев кроме общей формулировки, позволяющей определять направление векторного произведения или ориентацию базиса вообще, имеются специальные формулировки правила, особенно хорошо приспособленные к каждой конкретной ситуации (но гораздо менее общие).

В принципе, как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным, однако он должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, составляющие предмет этой статьи (они позволяют всегда придерживаться одного и того же выбора).

· Под названием правила правой руки существует несколько достаточно различающихся правил.

· Существует также несколько вариантов правила левой руки.

· В принципе можно ограничиться выбором из всего набора этих правил в разных формулировках (или из им подобных) какого-то одного, относящегося к универсальному типу (определению знака векторного произведения или ориентации базиса). Это минимально необходимый выбор (хотя бы один вариант правила нужен: без него вообще не только в принципе невозможно следовать общепринятым соглашениям, но и крайне трудно быть последовательным даже в собственных вычислениях). Но в принципе этого и достаточно: вместо всех правил, упоминаемых в этой статье или других им подобных в принципе^[3] можно пользоваться всего одним, если только знать порядок сомножителей в формулах, содержащих векторные произведения.

 

Общее (главное) правило

Главным правилом - которое может использоваться и в варианте правила буравчика (винта) и в варианте правила правой руки - это правило выбора направления для базисов и векторного произведения (или даже для чего-то одного из двух, т.к. одно прямо определяется через другое). Главным оно является потому, что в принципе его достаточно для использования во всех случаях вместо всех остальных правил, если только знать порядок сомножителей в соответствующих формулах.

Выбор правила для определения положительного направления векторного произведения и для положительного базиса (системы координат) в трехмерном пространстве — тесно взаимосвязаны.

Левая (на рисунке слева) и правая (справа) декартовы системы координат (левый и правый базисы). Принято считать положительным и использовать по умолчанию правый (это общепринятое соглашение, если только какие-то особые причины не заставляют от него отойти — и тогда это оговаривается явно).

Оба эти правила в принципе чисто условны^[4], однако принято (по крайней мере, если обратное явно не оговорено) считать, и это общепринятое соглашение, что положительным является правый базис, а векторное произведение определяется так, что для положительного ортонормированного^[5] базиса (базиса прямоугольных декартовых координат с единичным масштабом по всем осям, состоящего из единичных векторов по всем осям) выполняется^[6] следующее:

где косым крестом обозначена операция векторного умножения.

По умолчанию же общепринято использовать положительные (и таким образом правые) базисы. Левые базисы в принципе принято использовать в основном когда использовать правый очень неудобно или вообще невозможно (например, если у нас правый базис отражается в зеркале, то отражение представляет собой левый базис, и с этим ничего не поделаешь).

Поэтому правило для векторного произведения и правило для выбора (постороения) положительного базиса взаимно согласованы.

Они могут быть сформулированы так: