Как преобразовать комплексное число из алгебраической формы в экспоненциальную форму и наоборот. Приведите пример.

С алгебраической формой комплексного числа мы уже познакомились, 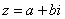– это и есть алгебраическая форма комплексного числа.

Любое комплексное число (кроме нуля) 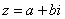можно записать в тригонометрической форме:
, где – это модуль комплексного числа, а 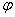– аргумент комплексного числа. Не разбегаемся, всё проще, чем кажется.

Изобразим на комплексной плоскости число 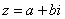. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что

Модулем комплексного числа 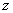называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длинарадиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа 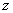стандартно обозначают: или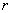

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: 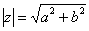. Данная формула справедлива для любых значений «а» и «бэ».

Пример 17.7 Пусть 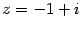. Напишите показательную форму числа .

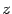Решение. Находим модуль и аргумент числа:

Следовательно, показательная форма комплексного числа такова:

 

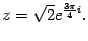
Пример 17.8 Комплексное число записано в показательной форме

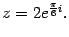
Найдите его алгебраическую форму.

Решение. По формуле Эйлера

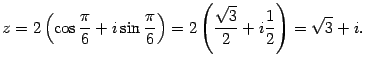
Итак, алгебраическая форма числа: .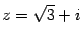

Распечатайте эти вопросы и запишите присланный регистрационный номер в левый верхний угол титульного листа.

Защищать работу можно у любого преподавателя кафедры «Высшая математика».

Расписание консультаций расположено в 7 корпусе рядом с аудиторией 7-310.