Округление чисел
Очень часто точное или приближенное число стремятся представить с числом цифр большим, чем это необходимо. Однако лишние цифры часто никакой существенной информации не несут, но затрудняют расчеты и измерение физических величин. В таких случаях производят округление. Но округление нужно выполнять правильно, исходя из выводов теории, во избежание недоразумений и неоднозначности толкования результатов округлений. Важность правил округления для практики даже закреплена стандартами, например, стандартом СТ СЭВ 543-77. Приведем сначала общие правила округления без учета погрешности.
Для записи приближенного числа используют только верные цифры. Неверные цифры отбрасывают, руководствуясь следующими правилами:
1. Если отбрасываемая цифра меньше 5, то последняя сохраняемая цифра не изменяется.
2. Если первая из отбрасываемых цифр больше 5, то последняя сохраняемая цифра увеличивается на единицу. Последняя сохраняемая цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр есть 5, а за ней есть одна или несколько цифр, отличных от нуля. Например, если число 0,3754 округляется до трех значащих цифр, то округленное число будет 0,375, а если до двух, то округленное число будет 0,38.
3. Если отбрасываемая цифра равна 5, а за ней нет значащих цифр, то последняя сохраняемая цифра остается неизменной, если она четная, и увеличивается на единицу, если она нечетная (правило четной цифры). Например, число 0,435 округляем до 0,44; а число 0,465 округляем до 0,46.
Очевидно, что в случае применения правил округления погрешность, обусловленная округлением, не превышает половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой. Поэтому, если данное число точное, то после правильного округления в записи числа все цифры будут верными.
Пример. Округляя число π = 3,1415926... до пяти, четырех и трех значащих цифр, получим приближенные числа: 3,1416; 3,142; 3,14 с абсолютными погрешностями, меньшими соответственно 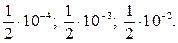
Округляя число 1,2500 до двух верных значащих цифр, получим приближенное число 1,2 с абсолютной погрешностью 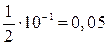 , а округляя точное число 8674 до двух верных значащих цифр, получим число 8700 с абсолютной погрешностью, меньшей
, а округляя точное число 8674 до двух верных значащих цифр, получим число 8700 с абсолютной погрешностью, меньшей 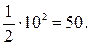
Если при записи приближенного числа необходимо учитывать погрешность, то порядок округления должен быть следующим.
1. Округление следует начинать с погрешности, оставляя в ней одну или две значащие цифры. Если первая цифра – единица или двойка, то после округления в записи погрешности оставляют две значащие цифры. Если же первая значащая цифра больше двойки, то в записи погрешности оставляют одну значащую цифру.
Примеры.
| До округления | После округления |
| 0,17295 | 0,17 |
| 4,8329 | |
| 0,97283 | 1,0 (именно так, а не просто 1, чтобы подчеркнуть, что погрешность погрешности заключена в первом знаке после запятой) |
| 0,006298 | 0,006 или 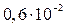 , или , или 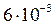 
|
| 384,53 | 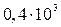 или или 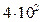 (но не 400 – ведь это уже 3 значащие цифры) (но не 400 – ведь это уже 3 значащие цифры)
|
2. Далее округляется сама вычисляемая или измеряемая величина. Причем ее последняя значащая цифра должна находиться в той же позиции, что и последняя значащая цифра погрешности.
Примеры.
| До округления | После округления |

| 
|
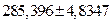
| 
|
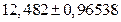
| 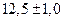
|
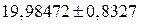
| 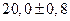
|
Из приведенных примеров видно, что если в погрешности присутствуют всего одна или две значащие цифры, то в самом результате после округления количество значащих цифр должно быть не меньше, чем в погрешности, причем последние значащие цифры в обоих числах стоят на одной и той же позиции.
3. Если при округлении погрешности указан множитель (порядок), т.е. 10n, то такой же порядок должен быть и у самой величины. При этом оба числа заключаются в скобки, и после них записывается множитель 10n.
Примеры.
| До округления | После округления |
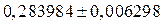
|  или
или 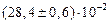 или
или 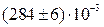
|
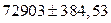
| 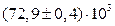 или
или 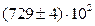
|
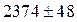
| 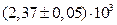 или или
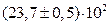
|