Что такое СКП случайной величины?
Средняя квадратическая погрешность (среднее квадратическое отклонение (Sд)) – характеристика рассеяния результатов измерений одной и той же величины вследствие влияния случайных погрешностей. Применяется для оценки точности первичных и вторичных эталонов. Она представляет среднюю квадратическую погрешность результата измерений, состоящую из случайных и неисключенных систематических погрешностей.
Наилучшим критерием оценки точности измерений принято считать среднюю квадратическую погрешность (СКП) измерения, определяемую по формуле Гаусса:
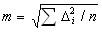
где Δi=li-X (Х - истинное значение измеряемой величины, а li - результат измерения).
Так как, в большинстве случаях истинное значение неизвестно, то СКП определяют по формуле Бесселя:
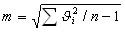
где ϑi=li-х (х - средняя арифметическое значение или вероятнейшее значение измеряемой величины, а li - результат измерения).
СКП арифметической середины:
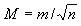
Эта формула показывает, что СКП арифметической середины в √n раз меньше СКП отдельного измерения.