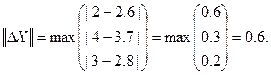Алгебра матриц, основные определения, норма матрицы

 

 

Система m*n чисел, расположенных в прямоугольной таблице из m строк и n столбцов

а₁₁ а₁₂ а₁₃…а_1n

а₂₁ а₂₂ а₂₃…а_2n

А=………………… ,

а_m1 а_m2 а_m3…а_mn

 

называется матрицей.

Матрица называется квадратной, если m= n. С квадратной матрицей связан определитель:

a₁₁ a₁₂ a₁₃…a_1n

a₂₁ a₂₂ a₂₃…a_2n

detA= ………………

a_m1 a_m2 a_m3…a_mn

 

Квадратная матрица называется вырожденной (особенной), если определитель ее равен нулю.

Под абсолютной величиной (модулем) матрицы A=(aij) будем понимать матрицу |A|=(|a_ij|), где |a_ij|- модули элементов матрицы А.

Если А и В- матрицы, для которых операции А+В и АВ имеют смысл, то:

1) |A+B|≤|A|+|B|;

2) |AB|≤|A||B|;

3) |αA|=|α||A|, где |α| - число.

Под нормой матрицы А понимается действительное число ||А||, удовлетворяющее условиям:

1) ||A||≥0, причем ||A||=0 тогда и только тогда, когда А=0;

2) ||αA||=|αA||;

3) ||A+B||≤||A||+||B||;

4) ||AB||≤||A|B||.

Рассмотрим три нормы матрицы:

1) m- норма, ||A||_m=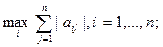

2) l- норма, ||A||_l=

3) k-норма, ||A||_k=

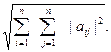
Пример: Вычислить нормы матрицы.

 

А= 1 -2

3 4

||A||_m=max(|1|+|-2|,|3|+|4|)=max(3,7)=7;

||A||_l=max(|1|+|3|,|-2|+|4|)=max(4,6)=6;

||A||_k=

Норма матрицы потребуется для оценки сходимости метода итераций.

Для проверки условия окончания итерационного процесса введем понятие нормы вектора и нормы вектора разностей.

Пусть дан вектор

 

Тогда в линейном пространстве Rⁿ n- мерных векторов норма вектора определяется:

 

||X||_m=max|x_i|;

||X||_l=|x₁|+|x₂|+…+|x_n| (2.1)

||X||_k= .

 

Пример. Вычислить нормы вектора

 

 

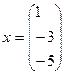
||X||_m=5; ||X||_l=|1|+|-3|+|-5|; ||X||_k=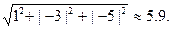

 

 

Пример. Вычислить норму вектора разностей

Пусть даны два вектора:

 

 

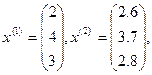
Норма вектора разностей x⁽¹⁾=x⁽²⁾ определяется: