Твердого тела. Замена опорной точки во втором ФЗМ
Уравнения первого и второго законов полностью описывают трансляционное и вращательное движения твердого тела:
 (5.31)
(5.31)
Второму уравнению можно придать более удобный для решения вид. Кинетический момент относительно неподвижной точки А можно выразить через кинетический момент относительно подвижной точки В (рис. 5.12,а):
 .
.
Аналогично  .
.
Подставляя эти выражения во второе уравнение (5.31), с учетом 
 , получим:
, получим:
 . (5.32)
. (5.32)
В некоторых случаях уравнение (5.32) проще и удобнее применять.
1. В качестве подвижной точки можно взять не принадлежащую телу точку, например, точку касания поверхности катящегося (или скользящего) тела (рис. 5.12,б). В этом случае  , поэтому уравнение (5.32) упростится:
, поэтому уравнение (5.32) упростится:
 ,
,
и, кроме того, в уравнение не войдут неизвестные реакции, поскольку их момент относительно точки В равен нулю.
2. Если в качестве подвижной точки В взять центр масс, уравнение (5.32) примет вид:  , или
, или
 . (5.33)
. (5.33)
Это уравнение полностью описывает вращательное движение и не отличается от уравнения, описывающего вращение вокруг неподвижной точки.
| Рис. 5.12. Подвижная опорная точка |
| A |
| ⦁ B |
| a) |
| C |

|

|

|
| B |
| б) |

|
| • C |
| в) |

|
| B |
| x |
| y |

|
| С Z |
Таким образом, удобной в большинстве случаев системой уравнений, описывающих произвольное движение твердого тела является следующая:
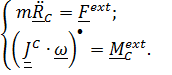 (5.34)
(5.34)
Если тело совершает плоское движение (рис 5.12,в), то  , где
, где  единичный вектор, перпендикулярный плоскости движения. Первое уравнение в (5.34) проецируется на оси
единичный вектор, перпендикулярный плоскости движения. Первое уравнение в (5.34) проецируется на оси  и
и  в плоскости движения, а второе скалярным умножением на
в плоскости движения, а второе скалярным умножением на  проецируется на ось
проецируется на ось  , проходящую через центр масс:
, проходящую через центр масс:  . С учетом
. С учетом  система имеет вид:
система имеет вид:
 (5.35)
(5.35)
Рассмотрим примеры.