Желілік график тиімдеу.

 

Желілік график – құрылып және есептеніп болғандықан кейін, желілік графиктің тиімдеуіне өтеміз. Тиімдеудің мақсаты желілік графиктің кейбір жұмыстардың жалғасуын және критикалық жолдың ұзындығын қысқарту болып табылады.

Тиімдеу 4 этаптарпен орындалады:

1. Критикалық жолда орналасқан жұмыстардың сандық сипаттамаларының дұрыстығын тексеру. Егер мүмкін болса, жұмыстарджың уақытын қысқартады. Бұл жұмыстардың ерекшіліктеріне байланысыты.

2. Критикалық жолда орналасқан жұмыстардың ресурстарын қысқартады. Босатылған ресурстарды критикалық жолда орналасқан жұмыстарға беріледі.

3. Егер технологиялық процесісне қатыспаса бірнеше жұмыстың паралелді орындалу мүмкіндіндік жүзеге асырылады.

4. Қосымша ресурстарды қолданудың мүмкіндіктердің қарастырамыз.

Осы 4 этап орынадалғаннан кейін желілік график қайта құрылады және есептеледі. Ал, желілік графиктің шығын есептерін және қайта есептелген, тиімделегн графикті салыстырамыз.

е.а

б.р

е.б

Бос резервті қысқарту:

R_ij=T_jk+T_ij

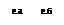T_ij=T_ij­+T_ij

		б.р

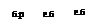R_ij=T_jk+T_ij+T_ij=>

T_ijá=R_ijâ

Баланстық модель.

 

Баланстық әдіс – бұл бар материалдық еңбектің ресурстарды және сол ресурстарға қажеттіліктерді сәйкестендіретін әдіс. Баланстық модель бұл теңдіктер жүйесі. Әр теңдік өңдірілетін өңімнің және сол өңімге қажеттілікті баланс талабын көрсетеді. Мысал келтірейік: екі өңім бірлікті қарастырайық. 1-нші өңімнің шикізаты болсын және жүйесінен тыс пайдаланады. Бұл жүйе бойынша баланстық сәйкестік W+X₂≤y_{1 ­}осындай түрде жазылады.Мұнда W-І өңімінің жүйеден тыс пайдалануы, Х₂ – 2 өңімге 1 өңімнің пайдалануы. у₂ -1-нші өңімнің жалпы шығарылуы.

Салааралық байланыс – бұл экономикалық жүйесінің салалардың ортасында байланыстарды сипаттайтые кесте.

 

Салалар			…	n	Итого	Конечная продукция	Валовая продукция
	X11	X12			Σx1j	Y1	X1
	X21	X22			Σx2j	Y2	Y1
...	…	…			…	…	…
N	Xn1	Xn2		Xnn	Σxnj	Yn	Xn
Итого	Σxi1	Σxi2		Σxin	ΣΣxij	Σyi	Σxi
Чистая продукция	V1	V2		Vn	ΣVj
Всего	X1	X2		Xn	ΣXj

Мұнда Xij j-нші өңімді өңдіру үшін i-нші өңімнің шығындары. Бірінші саласы – электроэнергия өңдірісі, баланстық екінші балансқа – көмір өңер кәсібі. Онда Х12 – көмір өңдіруге кететін шығындары, Х21- электр шығаруға кететін көмір шығындары. Xij – ақшалай есептеледі. Сондықтан осындай балансты бағалық баланс деп аталады. Ij=1…n, і-нші саланың басқа салаларға кеткен поставка көлемдері. Уі – і-нші саланың соңғы өңімі.

Хі = Σxij+yi

Σ xij –j-нші саланың өңдірістік шығындардың қосындысы. Vj – бұл условно чистая продукция.

Конф. Прямых затрат – аij

Aij = xij / xj

X1=(30+50)+100=180

X2=(80+80)+200=360

 

 

А11=30/180=1/6

А12=50/180=5/18

А21=80/360=2/9

А22=80/360=2/9

 

Баланстық модельдер Леоньтев В.В. 1923 жылы ойлап шығарды. «Модель затрат выпусков».

Сызықтық бағдарламалау.

Сызықты бағдарламалау 2 д.ж.с кезінде дами бастады. Осы уақытта ұйымдар мен өңдірісті жоспарлауда қажеттіліктер тіды. Негізінде өңдірісті жоспары әскери техникалардың қажетілік түсіндіру үшін қажет. Сызықты бағдарламалаудың тапсырмасы функцияның экстремуммын табумен сипатталады.

F(x)=C1+X1+ C2+X2+……+ Cn+Xn->max(min)

Мұнда:

C1, C2... Cn – коэффиценттер

Х1, Х2... Хn – белгісіз мәндер

Белгісіз мәндер Хn теріс таңбалы болмау керек немесе Х1, Х2; Хn≥0 бұл мәндер жүйеде берілген шектеулерді қанағаттандыру керек.

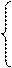A₁₁x₁+a₁₂x₂+…+A_1nx_n≥(=,≤)b₁

A₂₁x₁+a₂₂x₂+…+A_2nx_n≥(=,≤)b₂

A_n1x₁+a_n2x₂+…+A_nnx_n≥(=,≤)b₃

 

 

Шектеулер қатал немесе қатал емес болуы мүмкін. Шектеулер жүйесі барлық шешімдер мүмкін болатын шешімдер деп аталады. Егер нақты мүмкін болатын шешімдерде мақсатты функциягың мәні F(x) экстремумын тапса, онда мұндай шешім қолайлы шешім деп аталады.

Шешім барысында теңсіздіктер таңбасы теңдіктерге ауыстырылады. Бұл үшін шектеулер жүйесіне қосымша айнымалылар енгізіледі. Қосымша айнымалылардың индекстері қайталанбау керек. Егер шектеулерде ≥ танбасы тұрса онда қосымша айнымалылар – танбасымен енгізіледі.

Есепті шешу үшін базисті және базисті емес айнымалылардың саны, теңсіздіктердің санына тең болып қалады.

Мысалы:

=>

2x₁+3x₂≥10 2x1+3x2-x3=10

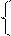
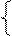
-10x₁-x₂8 -10x1-x2+x4=8

F(x)=2x1-x2=>max

 

Базисті	Базисті емес
1)X1,x2	X3=X4=0
2)x1,x3	X2=X4=0
3)x1,x4	X2=X3=0
4)x2,x3	X1=X4=0
5)x2,x4	X1=X3=0
6)x3,x4	X1=X2=0

 

№	X1	X2	X3	X4	F(x)≠2x1-x2->max
	-1,2	4,1			2*(-1,2)-4,1=-6,5
	-0,8		-11,6		X1<0
	2,22			6,4	F(x)=2*2.22=4.44
					F(x)=0-9=-9
		-0,5		11,3	F(x)=0-(-0.5)=0.5
					F(x)=0

Табылған шешімдерді кестеге толтырамыз.

 

№	X1	X2	X3	X4	F(x)
			-700
	566,8			466,6
				-525

 

СБЕ әдісімен әр-түрлі ңақты есептер шешіледі.

1. Өңдірісті жоспарлау.

2. Персоналды тағайындау.

3. Тиімді орналастыру есебі.

4. Диета құру есебі.

5. Транспорттық есебі.

Өңдірісті жобалау есебінің міндетті тұжырымдамасы:

Тігін шеберханасы 2 түрлі бұйымдар дайындайды. Көйлек және костюм. Көйлек 30 ақшалық бірлік, ал костюм 60 ақшалық бірлік тұрады. Бұйымдарды тігу кезінде 2 түрлі шикізат қолданылады. Жүн және жібек. Қоймада 21 метр жүн және 24 метр жібек бар. 1 көйлек тігу үшін 1 метр жүн және 3 метр жібек керек, ал 1 костюм тігу үшін 3 метр жүн және 2 метр жібек керек. Табыс максималды болу үшін қанша мөлшерде көйлек және костюм тігу керек.X1=көйлек мөлшері.Х2=костюмдер мөлшеріүХ1,х2≥0

 

F(x)=30*4+60*5=420

F(x)=80*8+60*13=240

F(x)=30*21+60*0=630

F(x)=30*0+60*12=720

F(x)=30*0+60*7=420

 

 

Мысал:

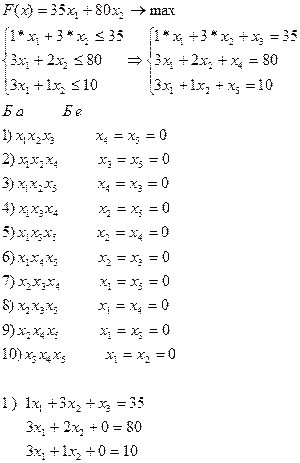
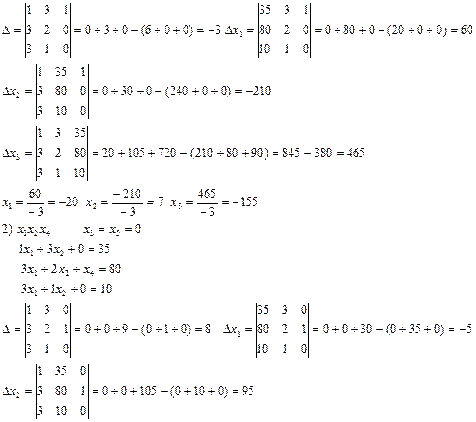
						F(x)
	-20		-155			–
	-0					–
			-66

 

СБЕ-ні графикалық шешуі.

 

СБЕ-ны шешуге арналған матрицалық тәсіл өте көп уақыт алады. Өте көп есептеулерді қажет етеді. Сондықтан СБЕ-ны шешу үшін графиклық тәсіл қолданылады. СБЕ-ні графикалық әдіспен шешу үшін шектеулер жүйесін графикалық түрге келтіреміз. Ол үшін түзулердің графигін сызамыз.

l1≈x1+3x2=21

l2≈3x1+2x1=24

 

 

 

X1	X2

X1	X2

 

 

Мүмкін болатын шешімдер аймағын табамыз. Ең тиімді шешім табу үшін Градиент вектор сызамыз. Бұл вектордың басы координат жүйесінің басында болады. Ал соңы мақсатты функцияның коэфиценттерінің нүктесінде болады. Мах мәнде табу үшін в-ға перпендикуляр түзу сызамыз. Перпендикуляр түзу түсіргенде ең жоғарғы нүктені тауып, оны максималды деп атаймыз. Осылайша таптық:

 

М = l1 ∩ l2

Табылған шешім шектеулер жүйесің қанағаттандыру керек және тексеру керек.

 

Симплекс ұғымы.

 

Сызықтық бағдарламалауда к.к. есебін шешетін Симплекс әдісі болып табылады. Қазіргі кезде қиын емес есептерді симплекс тәсілімен қолмен есептеп шығаруға болады. Симплекс тәсілінің негізінде берілген көпбұрыштығ төбелері тізбекті өтуде. Көпбұрыштың төбелерінің өтуі шектеулер жүйесі көмегімен жүзеге асырылады. Симплекс әдісінің алгоритмі:\

1. Егер шектеулер жүйесі теңсіздік түрінде берілсе, онда оны теңдік түріне келтіреміз.
2. Базисті және базисті емес айнымалыларды тандаймыз. Мақсатты функцияда айнымалылары бар айнымалыларды базисті емес деп атаймыз. Басқалар базисті.
3. 1-нші Симплекс кестені толтырамыз. Шектеулер жүйесінің коэфиценттері өз таңбасымен, ал мақсатты функцияның коэфиценттері қарама-қарсы таңбамен енгізіледі.

F(x)=2X1+3X2

F(x)=-2X1+3X2

1. Тиімді критерий бойынша кестені бағалаймыз.Егер мақсатты функция жолында теріс элементтер жоқ болса, онда функция экстремумына жетті деп санаймыз және табылған шешімді тиімді деп санаймыз да есептеулерді тоқтатамыз.
2. Тиімді критерий орындалмаса, онда шешуші бағанды табамыз. Ол үшін мақсатты фнукцияның коэфицентінен ең үлкен абсолютті санды табамыз. Сол баған шешуші баған болып табылады.
3. Шешуші баған бойынша бағалау қатынастарды есептейміз. Ол үшін бос мүшенің шешуші бағаның сәйкес келетін элементеріне бөлеміз. Шыққан сандардан ең кіші оң санын табу керек. Сол жол шешуші жол болып табылады.
4. Шешуші бағанмен жолдың қиылысында тұрған элементті шешуші элемент деп атаймыз. Оны 1-ге келтіреміз. Шешуші бағанның бойында тұрған басқа элементерді 0-ге келтіреміз. Кейінгі 4 қадамға ораламыз.
5. Тиімдік критерий орындалған кезде тиімді шешімді табамыз. Базисті емес айнымалыларды 0-ге теңейміз. Базисті айнымалырадың мәні 1-ге сәйкес келетін бос мүшенің мәніне тең.

 

Мысал: F(x)=2x1+3x2->max

 

X1+3X2≤18

2X1+X2≤16

X2≤5

3X1≤21

 

x1+3x2+x3=18 Базисті емес = x1,x2

2x1+x2+x4=16 Базисті = x3,x4,x5,x6

x2+x5=5

3x1+x6=21

 

Базисті	Бос мүше	Айнымалылар	Бағалау қатынастары
x1	x2	x3	x4	x5	x6
x3								16/3=6
x4								16/1=16
x5								5/1=5
x6								21/0=∞
F		-2	-3

Базисті	Бос мүше	Айнымалылар	Бағалау қатынастары
x1	x2	x3	x4	x5	x6
x3						-3		3/1=3
x4						-1		11/2=5,5
x5								5/0=∞
x6								21/3=7
F		-2

Тура және қосарлы есептер.

СБЕде кейбір кәсіпорындар шектеулі ресурстарды пайдаланып, максималды пайда табуды көздейді. Осы есеп үшін келесі СБЕ құрылады.

 

F=C₁X₁+ C₂X₂+… C_nX_n->max

Мұндағы с1,с2,сn – шикізаттардың бағалары, x1,x2,xn – тауарлардың мөлшері. Басқа жағынана сатып алушы кәсіпорын, дайын тауарларды тіп бағамен алғысы келеді. Ол үшін СБЕ есебі келесі түрде жазылады.

 

Z=b₁y₁+ b₂y₂+…+ b_ny_n->min

Мұндағы b1,b2,bn –сатып алатын шикізаттардың бағалары, x1,x2,xn – сатып алатын тауарлардың мөлшері. Бұл екі СБЕ-ң түрі қосарлы есеп деп аталады.

 

Тура есеп	Қосарлы есеп
F=C1X1+ C2X2+… CnXn->max	Z=b1y1+ b2y2+…+ bnyn->min
A11x1+a12x2+…+A1nxn≤b1 A21x1+a22x2+…+A2nxn≤b2 Am1x1+am2x2+…+Amnxn≤b3 x1≥0,x2≥0,xn≥0 Fmax	A11у1+a12у2+…+A1nуn≥)а1 A21у1+a22у2+…+A2nуn≥а2 An1у1+an2у2+…+Annуn≥а3 у1≥0,у2≥0,уm≥0 Zmin

Қосарланған есептердің қасиеттері:

1. Бір есепті мақсатты функция максимумға ұмтылса, оған қосарлы есепте минимумға ұмтылады.

2. Тура есептің мақсатты функциясы коэфиценттері қосарлы есебінің шектеулер жүйесінің бос мүшелері болып табылады.

3. Әр есеп канонды түрге келтірілген. Егер тура есептің шектеулер жүйесі = таңбасымен берілсе, онда қосарлы есепте шектеулер жүйесі ≥ таңбасымен беріледі.

4. Шектеулер жүйесінің коэфиценттердің матрицасының элементтері бір-біріне транспонерленген.

5. Осы екі есептердің айырмашылығы бір-біріне сәйкес болады.

6. Қосарлылық теоремасы. Егер тура есептің тиімді шешімі бар болса, онда лд қосарлы есептің тиімді шешіміне тең.

Транспорттық есеп.

 

Транспорттық есеп бұл сызықтық бғадарламалаудың ерекше сызықтық классы. Бұл есептерде барлық жеткізушілерден, барлық тұтынушыларға тауар жеткізу жоспарын құру қажет. Бұл жоспарда тұтынушылардың тұтыну және жектізушілердің жеткізушілік күші және құрылған жоспар бойынша құру керек.

Транспорттық есептің қойлымын бір мысал арқылы қарастырайық.

3 жеткізуші және 4 тұтынушы бар. Жеткізушілердің күштілігі және тұтынушылардың сұраныстары берілген. Жеткізушінің тауар бірлігінің жеткізунің шығыны берілген.

Жеткізуші және тұтынушы жұбы 1 жеткізу кестесіне енгізілген. Әр жұп үшін келесі шарттар орналуы тиіс:

1. Барлық жеткізушілердің күштілігі жүзеге асырылуы тиіс.

2. Әрбір тұтынушының сұранысы қанағаттандырылуы тиіс.

3. Жеткізушіге арналған шығындардың қосындысы минималды болуы тиіс.

Табылған СБЕ бойынша алдыңғы өткен әдістермен шешу қиын екенің көріп отырмыз. Сондықтан транспорттық есеп шешу үшін,өзіндік әдістер қолданамыз.

Транспорттық есеп шешудің 2 түрін қарастырамыз:

1. Жабық түрі – мұнда жеткізушілердің қүштілігі және тұтынушыларды сұранысымен бірдей болу керек. Яғни қарастырылған есеп, жабық түріне жатады.

2. Ашық түрі – мұнда жеткізушілердің суммарлық күші және тұтынушылардың сұраныстары бірдей болу тиіс.

Ашық түрдегі транспорттық есепті шешу үшін оны жабық түрге келтіреміз. Ол үшін фиктивті жеткізуші немесе тұтынушы кестеге енгізу керек. Оның күштілігі суммарлық күштіліктердің айырмашылығы тең болады.

 

 

Жет.№	Жет.күші	Тұтынушылар
		X11	X12	X13	X14
		X21	X22	X23	X24
		X31	X32	X33	X34

Ашық түрі.

60+120+70≠20+110+40+110 сондықтан

 

Жет.№	Жет.күші	Тұтынушылар
		x11	x12	x13	x14
		x21	x22	x23	x24
		x31	x32	x33	x34
4ф		x41	x42	x43	x44

Жабық түрі.

60+120+70+30 = 20+110+40+110

 

Солтүстік-батыс тәсілі бізге базисті шешімді береді. Бірақ бұл әдісінде тауар бірлігінің жеткізудің бағасы есепке алынбайды. Сондықтан басқа әдістер қолданады.

Мысал:

 

Жет	Жет күш	Тұтынушылар және сұраныстар
		2	3	4	8
		4	5	6	3
		4	3	4	2

 

50+80+70=200 40+50+30+40=160

200≠160

Енді оны жабық түріне кетіреміз:

200=160+40

Есепті жабық түрге келтіріп оны сол түстік батыс тәсілімен шешілуі:

 

Жет	Жет күш	Тұтынушылар және сұраныстар
				5 ф
				40
		2	3	4	8	0 0
		4	5	6	3	0 0
		4	3	4	2	40 0

Мақсатты функциясы:

F(x)=40*2+10*3+40*5+30*6+10*3+30*2=80+30+200+180+30+60=580

Минималды шығындар тәсілімен шығару:

Жет	Жет күш	Тұтынушылар және сұраныстар
				5 ф
				40
		2	3	4	8	0 0
		4	5	6	3	20 0
		4	3	4	2	20 0

Мақсатты функциясы:

F(x)=80+30+50+60+120+90+80=510

 

Оптималдысы ретінде минималды тәсілмен шығарылғанды айтамыз

Ол 510-ға тең.