Метод золотого сечения
Метод золотого сечения почти столь же эффективен, как и метод Фибоначчи, но при этом не зависит от N. Алгоритм поиска по методу золотого сечения определяется тем же правилом симметрии, что и алгоритм по методу Фибоначчи: на первой итерации выбираются две точки, расположенные симметрично относительно середины исходного отрезка; на каждой последующей итерации выбирается одна точка, расположенная симметрично оставшейся точки. Разница заключается в выборе точек. Метод золотого сечения основан на делении отрезка локализации «золотым сечением», т.е. таком делении, когда отношение большей части отрезка ко всему отрезку равно отношению меньшей части к большей
| C |
| B |
| A |

При таком делении используются две дроби Фибоначчи
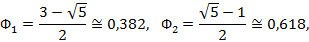
удовлетворяющие условиям

В случае метода золотого сечения используются два условия окончания вычислений:
а) выполнение заданного количества вычислений 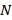 ,
,
б) достижение заданной величины 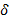 уменьшения отрезка локализации.
уменьшения отрезка локализации.
За одно вычисление функции отрезок, на котором находится xm, уменьшается в 1- 
 1.61 раза, т.е. быстрее, чем метод деления отрезка пополам.
1.61 раза, т.е. быстрее, чем метод деления отрезка пополам.
9. Сформулируйте общую задачу оптимизации.
Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. Постановка задачи оптимизации предполагает наличие объекта оптимизации, будь то человеческая деятельность в течение определенного периода времени или производственный процесс.
Математическое представление задачи проектирования называется общей формулировкой задачи оптимизации и может быть записано так:
Минимизировать целевую функцию F(x) , где x={  – проектные переменные.
– проектные переменные.
При этом должны выполняться:
· ограничения неравенства: 
· ограничения равенства: 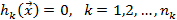
· ограничения области проектных переменных:  i=1,2,…,n
i=1,2,…,n
F(x) является скалярной функцией проектных переменных. Хотя проблема формулируется как задача минимума, мы легко можем искать и максимум функции, минимизируя её значение, умноженное на (-1).
10. Дайте классификацию задач оптимизации
Задача оптимизации это задача минимизации (максимизации) вещественнозначной функции 
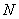 -мерного векторного аргумента
-мерного векторного аргумента 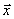 , компоненты которого удовлетворяют системе уравнений
, компоненты которого удовлетворяют системе уравнений 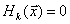 , и системе неравенств
, и системе неравенств  , а также ограничены сверху и снизу:
, а также ограничены сверху и снизу: 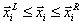 .
.
Функция  называется целевая функция.
называется целевая функция.
Уравнения 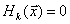 – функциональные ограничения в виде равенств.
– функциональные ограничения в виде равенств.
Уравнения  – функциональные ограничения в виде неравенств.+
– функциональные ограничения в виде неравенств.+
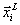 ,
,  – параметрические ограничения неравенств.
– параметрические ограничения неравенств.
Необходимо найти такое 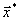 , которое доставляет минимальное или максимальное значение функции
, которое доставляет минимальное или максимальное значение функции  при всех ограничениях, причем
при всех ограничениях, причем  ,
, 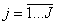 ,
,  . Такая задачаназывается условной оптимизацией.
. Такая задачаназывается условной оптимизацией.
Если 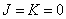 и пределы
и пределы 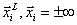 , то это задача безусловной оптимизации.
, то это задача безусловной оптимизации.
Задачи оптимизации классифицируются в соответствии с видом функций  ,
, 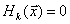 ,
,  и размерностью вектора
и размерностью вектора  .
.
Задачи без ограничений с  называются задачами одномерной оптимизации (
называются задачами одномерной оптимизации (  – многомерной оптимизации).
– многомерной оптимизации).
Если в задаче функции 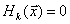 и
и  линейны, то это задача с линейными ограничениями.При этом целевая функция может быть как линейной, так и нелинейной.
линейны, то это задача с линейными ограничениями.При этом целевая функция может быть как линейной, так и нелинейной.
Задача условной оптимизации, в которой все функции линейны, называется задачей линейного программирования.
Задачи с нелинейными целевой функцией называются задачами нелинейного программирования.
Если  квадратичная, то задача квадратичного программирования. Если
квадратичная, то задача квадратичного программирования. Если  отношение линейных функций, то задача дробно-линейного программирования.
отношение линейных функций, то задача дробно-линейного программирования.
11. Сформулируйте принцип оптимальности Беллмана
Оптимальное поведение обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения.
Принцип оптимальности впервые был сформулирован Р. Беллманом в 1953 г. Каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. Беллманом четко были сформулированы и условия, при которых принцип верен. Основное требование — процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.
Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Если изобразить геометрически оптимальную траекторию в виде ломаной линии, то любая часть этой ломаной будет являться оптимальной траекторией относительно начала и конца.
12. Источники возникновения и распространения погрешностей
Источники погрешностей:
1) Погрешности, связанные с самой постановкой математической задачи (погрешности задачи, погрешности метода);
2) Погрешности, связанные с наличием бесконечных процессов в матанализе (остаточная погрешность);
3) Погрешности, связанные с наличием в формулах числовых параметров, значения которых могут быть определены лишь приближенно. Пр: все физические константы – начал. погрешность;
4) Погрешности, связанные с системой счисления – погрешность округления;
5) Погрешности, связанные с действиями над приближенными числами (погрешности
действий).
Причины возникновения погрешностей:
1) Приближенность математической модели
2) Погрешность входных данных
3) Погрешность метода решения
4) Погрешность машинного округления
Первые два вида — устранимые, последние два — неустранимые.
13. Охарактеризуйте особенности идентификации стохастических и динамических моделей.
(очень плохой вопрос)
Вар1. Идентификация динамических объектов в общем случае состоит в определении их структуры и параметров по наблюдаемым данным – входному воздействию и выходным величинам.
В этом случае объект (элемент системы, объект управления, элемент технологического процесса и т. п.) представляет собой "черный ящик". Исследователю необходимо, подвергая объект внешним воздействиям и анализируя его реакции, получить математическую модель (описание его структуры и параметров), то есть превратить "черный ящик" в "белый ящик", добиться его "информационной прозрачности". Графически процесс идентификации иллюстрирует рис. 1.
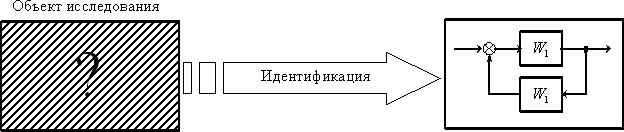
Рис. 1
Важным моментом этого процесса является выбор точек приложения внешних воздействий и сбор информации о реакциях объекта, то есть размещение управляющих устройств и датчиковых систем.
Решается при идентификации объектов и более простая (относительно простая) задача, это задача идентификации параметров, когда заранее известна структура математической модели объекта, но не известны ее параметры. В этом случае говорят о переходе от "серого ящика" к "белому ящику". Графически процесс идентификации параметров иллюстрирует рис. 2.

Рис. 2
Задача идентификации параметров может либо входить компонентом в общую задачу идентификации объекта, либо решаться самостоятельно.
Рассмотрим на обобщенной структуре и процедуре процесса идентификации основы подхода к решению задач идентификации. Обобщенная структура процесса идентификации показана на рис. 3.
Обобщенная процедура идентификации
- Классификация объекта.
- Выбор для определенного класса объекта настраиваемую модель, то есть модель, структуру и параметры которой можно менять в процессе идентификации.
- Выбрать критерий (оценку) качества идентификации, характеризующий в виде функционала доступных для наблюдения переменных отличие модели и объекта.
- Выбрать алгоритм идентификации (механизм настройки модели), обеспечивающий сходимость процесса идентификации, минимум критерия качества идентификации.

Рис. 3
Методы идентификации принято разделять на две группы:
- активная идентификация – идентификация вне контура управления,
- пассивная идентификация – идентификация в контуре управления.
Активная идентификация
В этом случае объект исследования выводится из условий нормальной окружающей среды (нормальный режим эксплуатации, номинальные параметры рабочего режима и т. п.). Исследования проводятся в специализированных лабораторных условиях, как это показано на рис. 4. На входы объекта (рабочие и дополнительные) подаются тестовые сигналы специального вида. Это могут быть:
- ступенчатые и импульсные временные сигналы,
- гармонические сигналы,
- случайные воздействия с заданными параметрами.
Активную идентификацию используют при разработке новых технологий применительно к действующим промышленным объектам, в изучении новых явлений, в первоначальной разработке математической модели.
Пассивная идентификация
При пассивной идентификации объект функционирует в контуре управления, находится в процессе нормальной эксплуатации. На его входы поступают только естественные сигналы управления.
Пассивную идентификацию используют для уточнения математической модели, для слежения за изменениями в объекте. Информация оперативно используется в системе управления объектом, процесс такой идентификации иллюстрируется рис. 5.

Рис. 4

Рис. 5
Или
Детерминированные объекты регулирования – объекты, в которых существует однозначная зависимость между входом и выходом.
В практике инженерных расчетов более распространенные экспериментальный метод получения математических моделей объектов управление. Позволяет получить математическое описание действующего объекта без исследования его внутренней структуры. Если существует однозначная зависимость между входами и выходами объекта, то получают детерминированную математическую модель. Задачами экспериментальных методов исследования динамики является выявление реакции объекта на возмущение определенной формы. Экспериментальные данные фильтруют от помех и заменяют (аппроксимируют) математическими выражениями.
Экспериментальные методы получения динамических моделей более простые, менее трудоемкие и более точные чем аналитические методы. Однако получены экспериментальным путем динамические характеристики конкретный объект не отображают внутренние взаимосвязи в объекте, и его структуру. Это не дает возможность результаты получены на конкретном объекте перенести на другие однотипные объекты.
В стохастических системах объект представляется в виде "черного ящика" – кибернетической системе, в которой единственной доступной информацией являются её входные и выходные переменные.
Аналитические методы математического моделирования базируются на наиболее общих законах природоведения: законах сохранения материи и энергии, зависимостях теплопередачи, гидростатики, гидродинамики и др.
Аналитические модели учитывают конструктивные характеристики объектов, их физико-химические и технологические особенности. Этот метод позволяет получить математические модели для действующих объектов, объектов что сооружаются и тех, которые только проектируются.
Основной недостаток аналитических моделей их недостаточная точность из-за упрощений и предположений, которые принимаются во время разработки модели.
Повышение точности таких моделей приводит к их осложнению, что затрудняет их использования на практике.
Идентификация – это процесс определения структуры и параметров математической модели, которые при одинаковых входных сигналах объекта и модели обеспечивают близость выхода модели к выходу объекта при наличии какого- либо критерия качества.
Методы идентификации разделяют на методы структурной идентификации и параметрической идентификации. Методы структурной идентификации предназначенные для определения структуры и параметров математической модели. В методах параметрической идентификации рассчитываются параметры модели известной структуры.
В методах параметрической идентификации вид математической модели выбирается на основе предыдущего анализа свойств объекта. Коэффициенты математической модели получают путем обработки и анализа экспериментальных данных. Результатом эксперимента является график динамической характеристики, который отображает реакцию исходной величины объекта моделирования на определенное возмущение.
Наиболее распространенным методом параметрической идентификации объектов управление является методом переходных характеристик. Этот метод базируется на исследовании поведения объекта управления после нанесения возмущения ступенчатой формы
14. Сформулируйте теорему Вейерштрасса о существовании решения задачи оптимизации
Одномерная задача оптимизации в общем случае формулируется следующим образом. Найти наименьшее (или наибольшее) значение целевой функции y=х, заданной на множестве σ, и определить значение проектного параметра х Є σ, при котором целевая функция принимает экстремальное значение. Существование решения поставленной задачи вытекает из следующей теоремы.
Теорема Вейерштрасса. Всякая функция F(х), непрерывная на отрезке [а, b], принимает на этом отрезке наименьшее и наибольшее значения, т.е. на отрезке [а, b] существуют такие точки х1 в х2, что для любого х Є [а, b] имеют место неравенства

Эта теорема не доказывает единственности решения. Не исключена возможность достижения равных экстремальных значений сразу в нескольких точках данного отрезка. В частности, такая ситуация имеет место для периодической функции, рассматриваемой на отрезке, содержащем несколько периодов.
Будем рассматривать методы оптимизации для разных классов целевых функций. Простейшим из них является случай дифференцируемой функции F(х) на отрезке [а, b], причем функция задана в виде аналитической зависимости у = F(х), и может быть найдено явное выражение для ее производной f’(x). Нахождение экстремумов таких функций можно проводить известными из курса высшей математики методами дифференциального исчисления. Напомним вкратце этот путь.
Функция f(x) может достигать своего наименьшего и наибольшего значений либо в граничных точках отрезка [а, b], либо в точках минимума и максимума. Последние точки обязательно должны быть критическими, т. е. производная f’(x) в этих точках обращается в нуль, — это необходимое условие экстремума. Следовательно, для определения наименьшего или наибольшего значений функции f(x) на отрезке [а, b] нужно вычислить ее значения во всех критических точках данного отрезка и в его граничных точках и сравнить полученные значения; наименьшее или наибольшее из них и будет искомым значением.
Случай, когда целевая функция задана в табличном виде или может быть вычислена при некоторых дискретных значениях аргумента, используются различные методы поиска. Они основаны на вычислении целевой функции в отдельных точках и выборе среди них наибольшего или наименьшего значений.
15. Дайте определение угловой точки выпуклого многогранного множества
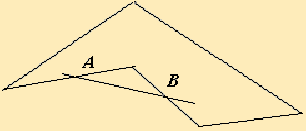
Точка выпуклого множества называется угловой (или крайней), если через неё нельзя провести ни одного отрезка, состоящего только из точек данного множества и для которого она была бы внутренней.
Для выпуклого многоугольника угловыми точками являются все его вершины. В пространстве выпуклое множество с конечным числом угловых точек называется выпуклым многогранником.
На рис. 2.1 изображено выпуклое множество (выпуклый многоугольник), а на рис. 2.2 - невыпуклое.
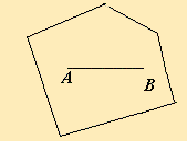
| 
|
| рис. 2.1 | рис. 2.2 |
Или
Точка х0 выпуклого многогранного множества М называется его угловой точкой (базисным допустимым решением), если она не лежит ни на каком отрезке, соединяющем какие-либо две точки множества М, отличные от нее. Угловые точки многогранника называются его вершинами.