Графическое определение равнодействующей плоской системы сил

Пусть дана плоская система трех сил: 1,2,3 (рис.7.1).

 

 

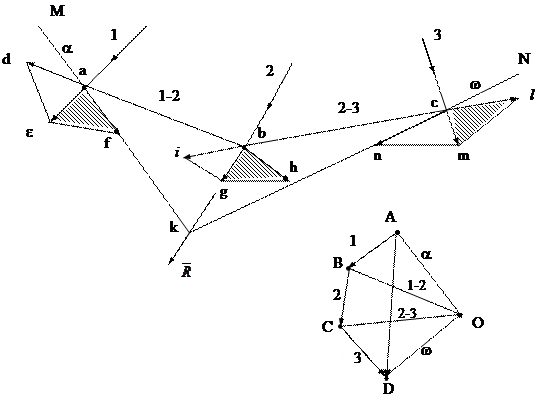Рис.7.1.

 

Построив силовой многоугольник, можно найти модуль и направление равнодействующей. (Построение надо производить, беря силы в определенном масштабе). Теперь нужно найти только линию действия данной равнодействующей.

Для этого выберем произвольную точку О, называемую полюсом, и соединим ее лучами со всеми вершинами силового многоугольника. Обозначим крайние лучи буквами a и w, а внутренние - через 1-2, 2-3, как это показано на чертеже. Затем из произвольной точки М, взятой недалеко от данной силы I, проведем прямую, параллельную лучу a силового многоугольника, до пересечения с линией действия силы I в точке а. Из точки а проведем прямую, параллельную лучу 1-2 до пересечения с линией действия силы 2 в точке b, из точки b проведем прямую, параллельную лучу 2-3 до пересечения с линией действия силы 3 в точке c, и наконец, из точки c проведем прямую, параллельную лучу w.

Ломанная линия MabcN называется веревочным многоугольником. Продолжим крайние стороны a и w веревочного многоугольника до их взаимного пересечения к точке k. Через точку k и будет проходить линия действия равнодействующей.

Докажем это. Перенесем силу 1 по линии ее действия в точку а и разложим ее на 2 составляющие, направленные по сторонам веревочного многоугольника.

Аналогично поступим с силами 2 и 3.

Поскольку Daef=DABO, то af=AO, ef=BO.

Далее Dbhg=DBCO, сдедовательно bh=BO, gh=CO.

Наконец, Dclm=DCDO, тогда cl=CO, ml=DO.

Отсюда ef=bh, gh=cl или ad=bh, bi=cl.

Итак, силы, направленные по сторонам 1-2, 2-3 веревочного многоугольника взаимно уравновешены и их можно отбросить. Остаются две силы и , следовательно, равнодействующая данной системы сил совпадает с их равнодействующей. Но линия действия этих двух пересекается в точке k, следовательно, через эту точку проходит и равнодействующая данной системы сил.