Математические схемы моделирования систем

 

При переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды применяют математическую схему как звено в цепочке «описательная модель – математическая схема – математическая (аналитическая или (и) имитационная) модель».

Модель объекта (системы S) можно представить в виде множества величин, описывающих процесс функционирования реальной системы:

• совокупность входных воздействий на систему

• совокупность воздействий внешней среды

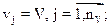
• совокупность внутренних (собственных) параметров систем

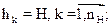
• совокупность выходных характеристик системы

Входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, а выходные характеристики являются зависимыми (эндогенными) переменными.

Процесс функционирования системы S описывается во времени оператором FS, который преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида

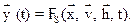(1)

Зависимость (1) называется законом функционирования системы F_S.

Математические модели называются динамическими (1), если математические соотношения описывают поведение объекта (системы) моделирования во времени t, т.е. отражает динамические свойства.

Для статических моделей математическая модель представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, H} в определенный момент, что в векторной форме может быть записано как

(2)

Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, т.е. если можно считать, что в этом случае стохастические воздействия внешней среды 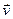(t) и стохастические внутренние параметры (t) отсутствуют, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями

(t)= f( 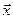, t). (3)

Очевидно, что детерминированная модель является частным случаем стохастической модели.

В практике моделирования объектов в области системотехники и системного анализа на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри, агрегативные системы и т.д.

При построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: непрерывно-детерминированный (D-схемы); дискретно-детерминированный (F-схемы); дискретно-стохастический (Р-схемы); непрерывно-стохастический (Q-схемы); сетевой (N-схемы); обобщенный или универсальный (А-схемы).