Отыскание правосторонней критической области

 

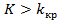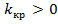Как найти критическую область? Обоснованный ответ на этот вопрос требует привлечения довольно сложной теории. Ограничимся ее элементами. Для определенности начнем с нахождения правосторонней критической области, которая определяется неравенством , где . Видим, что для отыскания правосторонней критической области достаточно найти критическую точку. Следовательно, возникает новый вопрос: как ее найти?

Для ее нахождения задаются достаточной малой вероятностью – уровнем значимости 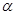. Затем ищут критическую точку , исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий примет значение, большее , была равна принятому уровню значимости:

 

Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию.

Почему правосторонняя критическая область была определена исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось соотношение

? (*)

Поскольку вероятность события 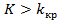, мала ( 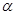-малая вероятность), такое событие при справедливости нулевой гипотезы, в силу принципа практической невозможности маловероятных событий, в единичном испытании не должно наступить. Если все же оно произошло, т.е. наблюдаемое значение критерия оказалось больше , то это можно объяснить тем, что нулевая гипотеза ложна и, следовательно, должна быть отвергнута. Таким образом, требование (*) определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они и составляют правостороннюю критическую область.