Лекция №9.
Комплексное сопротивление. Закон Ома
для цепи синусоидального тока.
Рассмотрим схему (рис.22), в которой резистор с сопротивлением R, катушка индуктивности с индуктивностью L и конденсатор ёмкостью С соединены последовательно. Схема питается от источника синусоидальной ЭДС.
| Рис.22. Электрическая схема. |

Запишем для данной схемы уравнение по второму закону Кирхгофа для мгновенных значений:
 (52)
(52)
Пользуясь выше приведённой таблицей перехода от мгновенных значений к комплексным изображениям, получим:
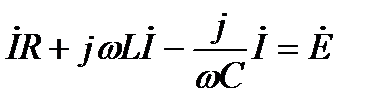 , (53)
, (53)
где  ,
, 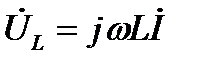 ,
, 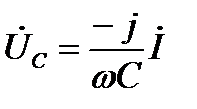 .
.
Направим вектор тока по вещественной оси комплексной плоскости и изобразим векторы напряжений на резисторе  , на катушке индуктивности
, на катушке индуктивности  , на конденсаторе
, на конденсаторе  на комплексной плоскости (рис.23):
на комплексной плоскости (рис.23):
| Рис.23. Векторная диаграмма цепи R,L,C. |

Получилась векторная диаграмма для рассматриваемой электрической схемы. Вектор напряжения на резисторе  совпадает по фазе с вектором тока
совпадает по фазе с вектором тока  , так как отсутствуют множители j или –j. Вектор Напряжения на катушке индуктивности
, так как отсутствуют множители j или –j. Вектор Напряжения на катушке индуктивности  из-за наличия множителя j повёрнут относительно вектора тока
из-за наличия множителя j повёрнут относительно вектора тока  против часовой стрелки на 90°, то есть в направлении положительного отсчёта углов. Вектор напряжения на конденсаторе
против часовой стрелки на 90°, то есть в направлении положительного отсчёта углов. Вектор напряжения на конденсаторе  из-за наличия множителя –j повёрнут относительно вектора тока по часовой стрелке на 90°, то есть в направлении отрицательно отсчёта углов. На этой векторной диаграмме
из-за наличия множителя –j повёрнут относительно вектора тока по часовой стрелке на 90°, то есть в направлении отрицательно отсчёта углов. На этой векторной диаграмме  ›
›  , поэтому в результате вектор тока
, поэтому в результате вектор тока  отстаёт на угол
отстаёт на угол  от вектора ЭДС
от вектора ЭДС 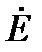 . В данном случае цепь имеет индуктивный характер.
. В данном случае цепь имеет индуктивный характер.
В выражении (53) вынесем ток за скобку:
 (54)
(54)
Множитель  представляет собой комплекс, имеет размерность сопротивления и обозначается
представляет собой комплекс, имеет размерность сопротивления и обозначается  . Его называют комплексным сопротивлением:
. Его называют комплексным сопротивлением:
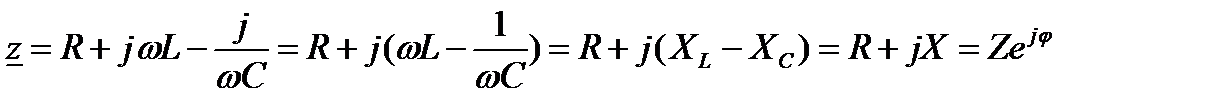 (55)
(55)
Здесь R -активное сопротивление цепи, 
 -реактивное сопротивление цепи, равное разности реактивного сопротивления катушки индуктивности
-реактивное сопротивление цепи, равное разности реактивного сопротивления катушки индуктивности 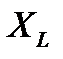 и реактивного сопротивления конденсатора
и реактивного сопротивления конденсатора 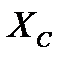 .
.
Уравнение (54) можно записать:
 (56)
(56)
или
 (57)
(57)
Уравнение (57) представляет собой закон Ома для цепи синусоидального тока.
| Рис.24. Векторная диаграмма цепи R,L,C |

Треугольник сопротивлений
Векторную диаграмму рис.23 изобразим несколько иначе, введя туда реактивное сопротивление цепи X (рис.24). На диаграмме получился треугольник 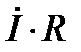 ,
, 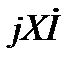 и
и  , причем везде входит комплекс тока
, причем везде входит комплекс тока  . Поделив на
. Поделив на 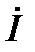 , получим треугольник сопротивлений R, X, Z.
, получим треугольник сопротивлений R, X, Z.
Изобразим отдельно треугольник сопротивлений:
| R |
| X |
| Z |

|

| Рис.25. Треугольник сопротивлений |
Для рис.25 можно записать:
 (58)
(58)
 (59)
(59)
 (60)
(60)
 (61)
(61)
 (62)
(62)
Комплексная проводимость
Под комплексной проводимостью 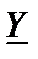 понимают величину, обратную комплексному сопротивлению
понимают величину, обратную комплексному сопротивлению  :
:
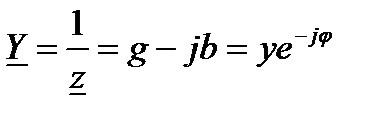 (63)
(63)
Действительную часть комплексной проводимости обозначают g, мнимую-b. Модуль комплексной проводимости обозначают y. Так как 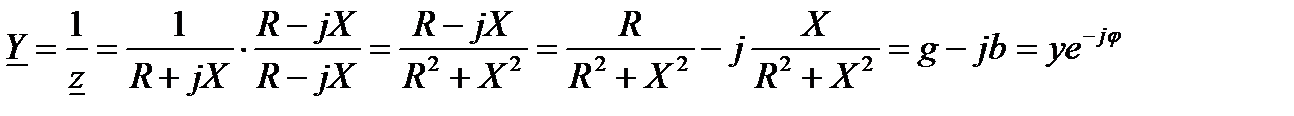 , то
, то

 ,
,  (64)
(64)
При использовании комплексной проводимости закон Ома записывается так:
 (65)
(65)
Изобразим векторную диаграмму для схемы рис.22 с использованием комплексной проводимости (рис.26):

Рис.26. Векторная диаграмма.
Получился прямоугольный треугольник, где  и
и 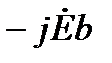 - катеты, а
- катеты, а  - гипотенуза.
- гипотенуза.
Треугольник проводимостей
Поделив все три стороны треугольника на 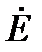 , получим треугольник проводимостей g, b, y (рис.26).
, получим треугольник проводимостей g, b, y (рис.26).
Изобразим отдельно треугольник проводимостей:
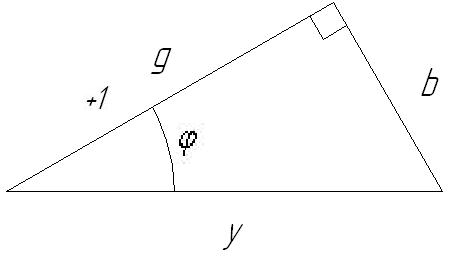
Рис.27. Треугольник проводимостей.
Для рис.27 можно записать:
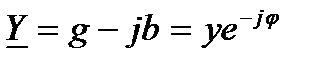 ; (66)
; (66)
 (67)
(67)
 (68)
(68)
 ; (69)
; (69)
 ; (70)
; (70)
Объединим векторные диаграммы рис.24 и рис.26 (рис.28);

Рис.28. Векторная диаграмма.
Операции с комплексными числами при расчёте цепей синусоидального тока
Любое комплексное число может быть записано в трёх формах: алгебраической, показательной и тригонометрической. Например:
 (71)
(71)
 -алгебраическая форма записи комплексного числа.
-алгебраическая форма записи комплексного числа.
 -показательная форма записи комплексного числа.
-показательная форма записи комплексного числа.
 -тригонометрическая форма записи комплексного числа.
-тригонометрическая форма записи комплексного числа.
На калькуляторе сложение, вычитание, умножение и деление комплексных чисел производится в алгебраической форме.
Ответ желательно иметь в двух формах: алгебраической и показательной. Комплексные сопротивления достаточно иметь в алгебраической форме для проведения расчётов. А вот комплексы токов ветвей, напряжений на отдельных участках схемы нужно обязательно перевести в показательную форму, так как переход от комплексных изображений к мгновенным значениям (синусоидам) производится от показательной формы.
Тригонометрическая форма записи является промежуточной и служит для перехода от показательной формы к алгебраической.
Покажем на примере расчёты с комплексными числами.
Прежде всего переключатель на калькуляторе DRG поставить в положение DEG, что означает измерение угла  в показательной форме в градусах.
в показательной форме в градусах.
Другие два положения переключателя: RAD-радианы, GRAD-грады.
Далее нужно определиться с точностью расчёта: сколько знаков после запятой мы хотим иметь. Так, если требуется делать расчёты, с точностью три знака после запятой, то мы нажимаем следующие клавиши:
| TAB |
2ndf 3
Чтобы вернуться в обычный режим, надо нажать следующие клавиши:
| TAB |
2ndf
Произведём расчеты следующего комплексного выражения:
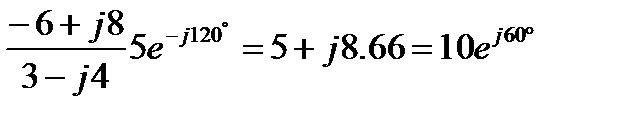
Так как калькулятор считает комплексы только в алгебраической форме, то прежде всего комплексное число 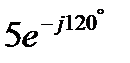 надо из показательной формы перевести в алгебраическую.
надо из показательной формы перевести в алгебраическую.
Включаем калькулятор, устанавливаем углы в градусах, точность расчёта, например, три знака после запятой и далее нажимаем клавиши:
| CPLX |
2ndf
Калькулятор перешёл в режим расчёта комплексных чисел. В правом верхнем углу возникает надпись CPLX.
Далее нажимаем:
2ndf a 5 a -120 b
2ndf a Калькулятор подготовлен к введению комплексного числа в показательной форме.
5 a -120 b вводится модуль комплекса 5 и угол -120º комплексного числа.
Далее нужно перевести введённое комплексное число в показательной форме в алгебраическую форму, чтобы калькулятор мог делать расчёты.
Для этого нажимаем дальше клавиши:
2ndf b Комплексное число  переведено в алгебраическую форму.
переведено в алгебраическую форму.
Далее нажимаем:
x -6 a 8 b
Умножили предыдущий комплекс на комплексное число -6+j8.
Далее нажимаем:
: 3 a -4 b
Разделили предыдущий результат на комплексное число 3-j4.
Далее нажимаем:
= И получаем ответ в алгебраической форме 5+j8,66.
Чтобы перевести ответ в показательную форму, нажимаем клавиши:
2ndf а Получаем ответ в показательной форме 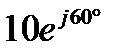 .
.
Никаких промежуточных записей не делаем. Только ответы в алгебраической и показательной форме.
На некоторых калькуляторах вместо клавиши 2ndf стоит клавиша shift того же назначения.
Законы Кирхгофа в комплексной форме
Все методы расчёта, рассмотренные в линейных цепях постоянного тока полностью применимы в цепях синусоидального тока. Правила составления уравнений, правила знаков те же самые, что и в цепях постоянного тока.
Рассмотрим схему рис.29.
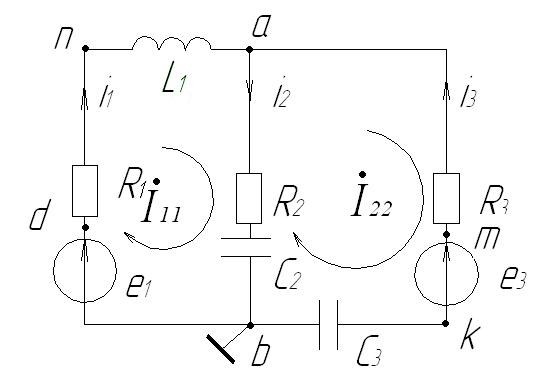
Рис.29. Электрическая схема.
В схеме рис.29 два узла “а” и “в”, и два независимых контура “abdna” и “amkba”.
По первому закону Кирхгофа нужно составить уравнения, равное числу узлов без единицы, то есть в данном случае одно уравнение. Число уравнений по второму закону Кирхгофа равно числу независимых контуров. Запишем сначала эти уравнения для мгновенных значений, то есть в дифференциальной форме.
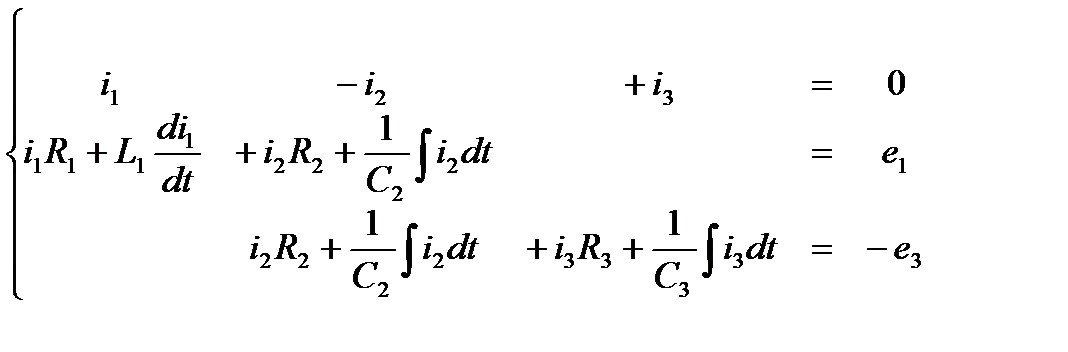 (72)
(72)
Пользуясь вышеприведённой таблицей для перехода от мгновенных значений к комплексным изображениям, получим:
 (73)
(73)
Система уравнений (73) записана теперь в алгебраической форме, решать которую значительно проще.
 (74)
(74)
Получилась окончательная форма записи системы уравнений в комплексной форме по первому и второму законам Кирхгофа.
Метод контурных токов в комплексной форме записи
Выберем направления контурных токов по часовой стрелке в обоих независимых контурах. В схеме рис.29 два независимых контура. Составим уравнения по методу контурных токов.
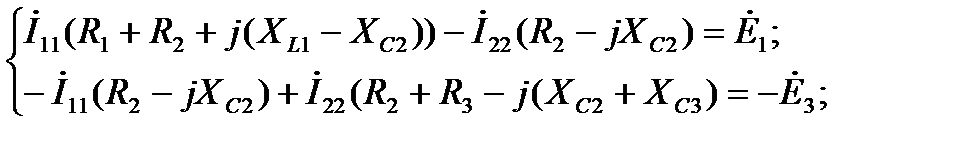 (75)
(75)
Взаимное комплексное сопротивление  взято со знаком “минус”, потому что контурные токи во второй ветви направлены навстречу друг другу.
взято со знаком “минус”, потому что контурные токи во второй ветви направлены навстречу друг другу.
После того, как будут найдены контурные токи  и
и  , можно найти токи в ветвях:
, можно найти токи в ветвях:


 (76)
(76)
Метод узловых потенциалов в комплексной форме записи
Заземлив узел “b”, т.е.  . В этом методе нужно составить всего одно уравнение:
. В этом методе нужно составить всего одно уравнение:
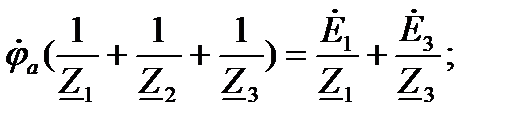 (77)
(77)
Здесь  =
=  ;
; 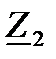 =
=  ;
; 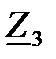 =
=  .
.
Правило знаков такое же как на постоянном токе. ЭДС  направлена к узлу “a”, поэтому
направлена к узлу “a”, поэтому  будет со знаком “плюс”, ЭДС
будет со знаком “плюс”, ЭДС  также направлена к узлу “a”, поэтому
также направлена к узлу “a”, поэтому  будет со знаком “плюс”.
будет со знаком “плюс”.
После того, как найден потенциал узла “a”, можно найти комплексы всех токов:
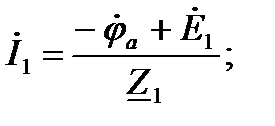
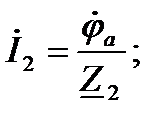
 ; (78)
; (78)
Метод активного двухполюсника и эквивалентного генератора
Предположим, надо найти комплекс тока  , не определяя остальные токи. Осуществим в первой ветви режим холостого хода, для чего уберём комплексное сопротивление
, не определяя остальные токи. Осуществим в первой ветви режим холостого хода, для чего уберём комплексное сопротивление  .
.
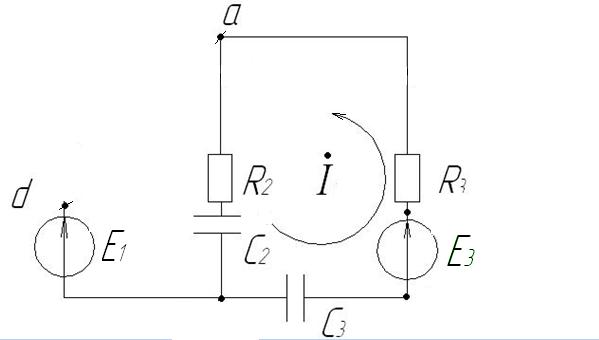
Рис.30. Режим холостого хода.
Согласно методу активного двухполюсника и эквивалентного генератора.
 (79)
(79)
В схеме рис.30 протекает ток  , который можно найти по закону Ома:
, который можно найти по закону Ома:
 (80)
(80)
Теперь можно определить ЭДС холостого хода 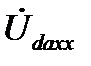 , т.е. ЭДС эквивалентного генератора:
, т.е. ЭДС эквивалентного генератора:
 (81)
(81)
Входное сопротивление  можно определить по схеме рис.30, если идеальные источники ЭДС
можно определить по схеме рис.30, если идеальные источники ЭДС  и
и  закоротить, так как их внутреннее сопротивление равно нулю.
закоротить, так как их внутреннее сопротивление равно нулю.
Получается следующая схема (рис.31):
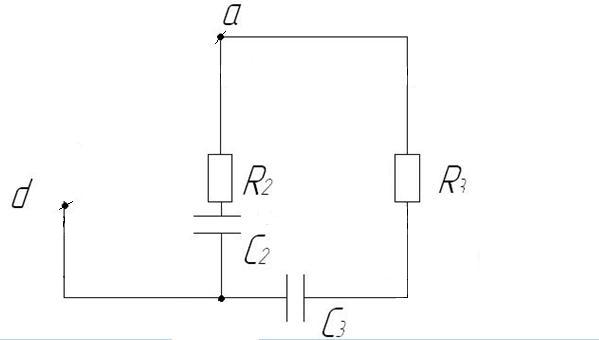
Рис.31. Схема пассивного двухполюсника
По схеме рис.31 можно записать:
 (82)
(82)
И теперь по формуле (79) можно найти комплекс тока  .
.