Взаимная информация

Таким образом, мы можем определить количество информации о системе Х, ведя наблюдение непосредственно за системой Х. На практике часто бывает, что система Х для наблюдения не доступна, и тогда ведут наблюдение за другой системой Y, как-то связанной с системой Х. Например, вместо непосредственного наблюдения за космическим кораблем ведется наблюдение за системой сигналов, передаваемых его аппаратурой. Или наблюдение за футбольным матчем по телевизору.

Между системой X и Y имеются различия, которые могут быть двух видов:

1.Различия за счет того, что некоторые состояния системы X не находят отражения в системе Y (Y менее подробна, чем система X).

2.Различия за счет ошибок: неточностей измерения параметров системы X и ошибок при передаче сообщений.

Например, в черно-белом телевидении теряется цвет; влияние помех, которые вносят искажения.

То есть система Y отличается от системы X. Возникает вопрос: какое количество информации о системе X дает наблюдение системы Y? Данную информацию определяют как уменьшение энтропии системы X в результате получения сведений о системе Y.

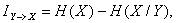(1.11)

где H(X) - априорная энтропия до наблюдения, H(X/Y) - остаточная энтропия, после получения сведений, - полная или средняя информация о системе X, содержащаяся в системе Y.

В общем случае, при наличии двух систем, каждая содержит относительно другой системы одну и ту же полную информацию. Покажем это:

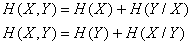
откуда

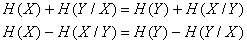
- называется полной взаимной информацией содержащейся в системах X и Y.

Посмотрим, во что обращается полная взаимная информация в крайних случаях полной независимости и полной зависимости систем. Если X и Y независимые системы, то H(Y/X)=H(Y), и =0. Это и понятно, так как нельзя получить сведений о системе, наблюдая вместо нее другую систему, никак с нею не связанную.

Другой крайний случай X и Y полностью определяют друг друга, то есть совпадают. Тогда H(X)=H(Y), H(X/Y)=H(Y/X)=0

и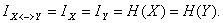

Рассмотрим случай, когда между X и Y имеется жесткая зависимость, но односторонняя: состояние одной из систем полностью определяет состояние другой, но не наоборот. По состоянию подчиненной системы вообще нельзя однозначно определить состояние другой. Очевидно, энтропия подчиненной системы меньше чем та, которой она подчиняется, так как она менее подробна. Тогда полная взаимная информация, содержащаяся в системах, из которых одна является подчиненной, равна энтропии подчиненной системы.

Пусть из двух систем X и Y подчиненной является Y. Тогда H(Y/X)=0, и

Таким образом, полная взаимная информация, содержащаяся в системах, из которых одна является подчиненной, равна энтропии подчиненной системы.

Выведем выражение для информации не через условную энтропию, а через энтропию объединенной системы 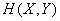и энтропию отдельных ее частей H(X), H(Y).

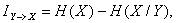
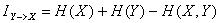
Выразим полную взаимную информацию через вероятности состояний системы. Для этого запишем значения энтропии отдельных систем через математическое ожидание:

H(X)=M[-log P(X)], H(Y)=M[-log P(Y)], H(X,Y)=M[-log P(X,Y)]

Тогда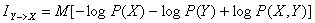

и далее

(1.12)

Таким образом, получили полную взаимную информацию об одной системе X с помощью другой системы Y. (Информация “от системы к системе”). Кроме полной взаимной информации существуют и частные виды взаимной информации. Выражение (1.12) представим в виде

Тогда, вторая сумма и будет представлять частную информацию о системе X, получаемую с помощью отдельного события системы Y.

(1.13)

Выражение (1.13) представляет частную информацию “от события к системе”. Далее можно определить частную информацию о событии x_i, содержащуюся в событии y_j (информация “от события к событию”):

_(1.14)

Информация 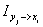симметрична