Статистический анализ тестовых результатов и отбор заданий

для включения в тесты

В табл. 3.5 приведены некоторые показатели, рассчитанные по результатам пробного тестирования.

Таблица 3.5 - Анализ результатов тестирования*[10]

ПОКАЗАТЕЛИ Номер задания

Кол-во правильных ответов

Кол-во неправильных ответов

Доля правильных ответов, p_j 0,8 0,7 0,6 0,5 0,5 0,4 0,3 0,2

Доля неправильных ответов, q_j 0,2 0,3 0,4 0,5 0,5 0,6 0,7 0,8

Потенциал трудности, q_j/p_j 0,00 0,25 0,43 0,67 1,00 1,00 1,50 2,33 4,00 -

Дисперсия баллов, p_j×q_j 0,16 0,21 0,24 0,25 0,25 0,24 0,21 0,16

Коэффициент корреляции баллов по заданию с суммарными баллами по всему тесту - 0,41 0,62 0,75 0,82 0,82 0,75 0,62 0,41 -

Наиболее важными из приведенных в табл. 3.5 показателями являются:

1) потенциал трудности;

2) дисперсия баллов;

3) коэффициент корреляции баллов по заданию с суммарными баллами по всему тесту.

Именно эти показатели являются критериями, по которым можно судить о том, может ли задание в тестовой форме использоваться в тестах, т.е. называться тестовым заданием.

Первый показатель соответствует требованию (см. раздел 1.2) известной трудностизадания. Как видно из табл. 3.5, этому требованию не соответствуют задания №1 и №10, что подразумевает необходимость их «ревизии» разработчиком с целью выявления причин (задание слишком легкое или слишком трудное, неверно сформулировано, содержит «подсказку» в вариантах ответов, неверно воспринимается испытуемыми и т.п.). После «ревизии» задание либо перерабатывается, либо исключается и в тестах не используется.

Не менее важна и дисперсия баллов, которая может служить показателем дифференцирующей способностизадания, т.е. его способности разделить группу испытуемых на сильных и слабых. Чем больше дисперсия баллов, тем лучше дифференцирующая способность задания. Однако, задания с невысоким значением дисперсии (например, задания №2 и №9) также могут использоваться в тестах (с учетом значения коэффициента корреляции с суммарными баллами по всему тесту). Такие задания позволяют более четко отделить совсем неподготовленных от тех, кто знает на «3» и, соответственно тех, кто знает на «5», от тех, кто «не дотягивает» до максимальной оценки.

Третий показатель – коэффициент корреляции баллов по заданию с суммарными баллами по всему тесту, является наиболее важным. Если его значение невелико, то без соответствующего задания в тесте, видимо, можно обойтись. Напротив, задания с большим значением указанного коэффициента (выше 0,7) могут считаться «ведущими» или «тестообразующими» заданиями, «ключевыми» для данной дисциплины или ее раздела. Рекомендуют включать задание в тест при том условии, что коэффициент корреляции составляет величину не ниже 0,25-0,3.

Для вычисления коэффициента корреляции в нашем случае наиболее удобной представляется формула [6]

,

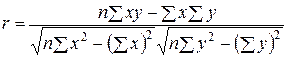где 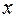- балл за задание; - суммарный балл по тесту; - количество испытуемых в группе.

Рассчитаем для примера коэффициент корреляции балов по заданию №5 с суммарными тестовыми баллами применительно к приведенной в табл.3.4 матрице тестовых результатов (см. табл. 3.6).

Таблица 3.6 – Расчет коэффициента корреляции

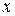
Испытуемый	Балл за задание №5,	Суммарный балл по тесту,
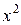
1. Абрамов
2. Дмитриев
3. Васильев
4. Борисов
5. Щетинин
6. Зыков
7. Григорьев
8. Кириллов
9. Иванов
10. Жуков
S

Отсюда

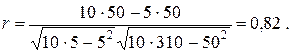
При использовании для анализа тестовых результатов компьютерной техники целесообразно воспользоваться для расчета коэффициентов корреляции соответствующей функцией табличного процессора Excel.

Не менее важно и сопоставление результатов тестирования, полученных в параллельных (различных) группах. Такое сопоставление производится путем сравнения потенциалов трудности, дисперсий и коэффициентов корреляции баллов по заданиям с суммарными баллами по тесту, которые в идеале должны отличаться незначительно. Существенные отличия указанных показателей могут свидетельствовать либо о невысокой воспроизводимости тестовых результатов (т.е. на одинаковых по уровню группах один и тот же тест дает различные результаты), либо о существенно различающемся уровне подготовленности испытуемых в разных группах (т.е. группы не являются параллельными).

Проверку параллельности групп можно произвести путем оценки однородности дисперсий суммарных тестовых результатов, используя соответствующие статистические критерии - Фишера, Кочрена, Бартлета [7]. По этим критериям можно при достаточно высоком уровне значимости (рекомендуется 0,05) проверить, насколько параллельные группы отличаются по среднему уровню подготовленности.

Еще одним приемом, который можно использовать при обработке результатов тестирования, является объединение результатов тестирования параллельных групп. Этот прием рекомендуется использовать при небольшом числе испытуемых в отдельных группах, но перед «объединением» результатов желательно произвести проверку однородности дисперсий по критериям, упомянутым выше.