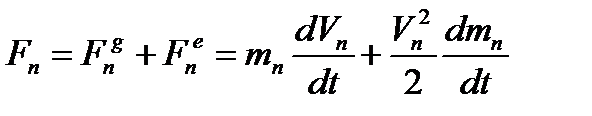Уравнение движения звена приведения в энергетической и дифференциальной формах.
В результате приведения сил и масс реальную схему механизма заменяют упрощенной динамической моделью с вращающимся или поступательным звеном приведения
Уравнение движения показывает зависимость силовых параметров Mn (или Fn) от инерционных In (mn) или кинематических q, V или w, a или 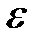 . Уравнение движения может записываться в дифференциальной или интегральной формах.
. Уравнение движения может записываться в дифференциальной или интегральной формах.
Уравнение в дифференциальной форме основано на равенстве дифференциалов элементарных работ dA и дифференциалов кинетической энергии dT в любой момент времени: dA=dT.
Покажем для вращающегося звена приведения:
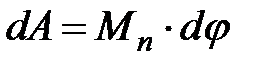 ;
; 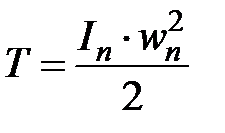 ;
; 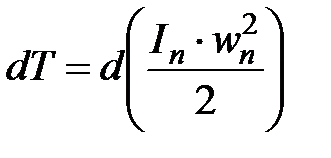 ;
; 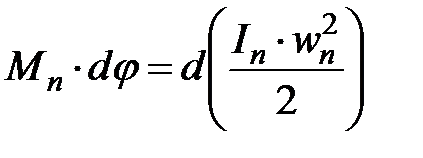

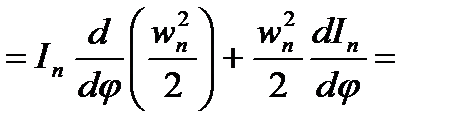

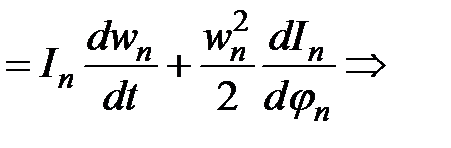
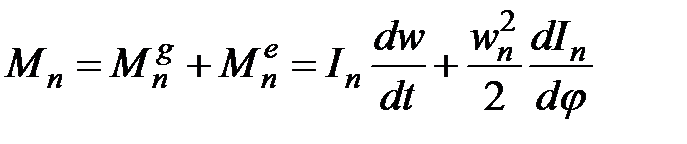 ;
;
Аналогично можно получить для поступательного звена приведения