Указания к выполнению работы.
Метод хорд применим на отрезке изоляции корня  , если выполняются условия:
, если выполняются условия: 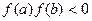 ;
;  ,
,  и
и  существуют;
существуют;  и
и  сохраняют знак на
сохраняют знак на  .
.
В задании 2-1 необходим предварительный анализ функции на знак второй производной и знак самой функции на выделенном отрезке неопределенности. Находим ту границу найденного отрезка неопределенности  , для которой знак функции
, для которой знак функции  совпадает со знаком ее второй производной
совпадает со знаком ее второй производной  . Эта граница отрезка неопределенности в процессе его сужения остается неподвижной, если
. Эта граница отрезка неопределенности в процессе его сужения остается неподвижной, если  сохраняет знак на всем исходном отрезке. Другая граница интервала изменяется и определяется по формуле координаты пересечения хорды с осью 0x. По условию задания 2-1 необходимо сделать только заданное число шагов.
сохраняет знак на всем исходном отрезке. Другая граница интервала изменяется и определяется по формуле координаты пересечения хорды с осью 0x. По условию задания 2-1 необходимо сделать только заданное число шагов.
В задании 2-2 после нахождения исходного отрезка  внутренняя точка определяется по формуле
внутренняя точка определяется по формуле  , после чего эта точка (в зависимости от результатов анализа произведения значений функции на границах
, после чего эта точка (в зависимости от результатов анализа произведения значений функции на границах  ) становится одной из границ нового отрезка. Остановку производят на основе анализа расстояния между двумя последними решениями. Расчеты следует оформить в виде представленной ниже таблицы.
) становится одной из границ нового отрезка. Остановку производят на основе анализа расстояния между двумя последними решениями. Расчеты следует оформить в виде представленной ниже таблицы.
| 
| 
| 
| 
| 
| 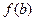 
| 
| 
| Условие
остановки по 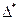
| Условие
остановки по 
|
Столбцы содержат: 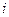 – номер шага;
– номер шага;  – начало отрезка;
– начало отрезка;  – конец отрезка;
– конец отрезка;  - внутренняя точка последнего отрезка (пересечение хорды с осью 0x);
- внутренняя точка последнего отрезка (пересечение хорды с осью 0x);  ,
,  ,
, 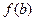 - значения функции в соответствующих точках;
- значения функции в соответствующих точках; 
 - абсолютная погрешность текущего решения;
- абсолютная погрешность текущего решения; 
 - относительная погрешность текущего решения. Первая строка расчетной таблицы не содержит формулы для определения текущих значений погрешностей и формулы анализа остановки. При такой организации вычислительного процесса предварительно определять неподвижную границу не нужно.
- относительная погрешность текущего решения. Первая строка расчетной таблицы не содержит формулы для определения текущих значений погрешностей и формулы анализа остановки. При такой организации вычислительного процесса предварительно определять неподвижную границу не нужно.
Если исходный отрезок найден правильно (соблюдаются указанные выше требования к функции, ее первой и второй производным), то в расчетной таблице одна из границ отрезка неопределенности остается постоянной. Для удобства можно ввести дополнительный столбец  для анализа знака произведения, используемого при принятии решения о сужении отрезка.
для анализа знака произведения, используемого при принятии решения о сужении отрезка.
По условию задания 2-2 процесс вычислений следует прекратить при выполнении неравенств  и
и  . В качестве решения следует выбрать последнюю найденную точку
. В качестве решения следует выбрать последнюю найденную точку  .
.