Действия над матрицами

1. Суммой двух матриц и одного порядка называется матрица , каждый элемент которой равен сумме соответствующих элементов матриц А и В.

Из определения следует, что выполняются операции коммутативности сложения A+B=B+A и ассоциативности сложения A+(B+C)=(A+B)+C.

2. При умножении матрицы на число k каждый ее элемент умножается на это число.

Отсюда следует, что общий множитель всех элементов матрицы можно вынести за знак матрицы.

Операция умножения матрицы на число обладает свойствами:

(α+β)А=αА+β;

α (А+В)= αА+ αВ,

где α и β – числа.

3. Умножение матриц. Пусть заданы матрицы и .

Произведением A×B называется матрица C порядка m×k:

А·В= 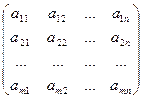· =С= ,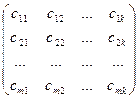

элементы которой вычисляются по формулам:

;

и т.д.

Операция перемножения матриц не коммутативна, то есть АВ≠ВА.

4. Транспонирование матрицы - это операция, при которой строки матрицы становятся столбцами, и наоборот.

Пример. Найти матрицу С=В(3А-2В), где А= и В= .

Решение. 1) Найдем матрицу (3А-2В)= 3 - 2 = - = .

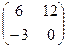2) С=В(3А-2В) = = .