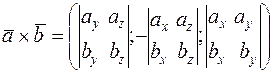Векторное произведение векторов.

 

Векторным произведением векторов называется вектор , определяемый условиями:

1) вектор перпендикулярен векторам , т.е.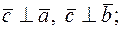

2) длина вектора равна площади параллелограмма, построенного на векторах как на сторонах, т.е.

3)векторы и образуют правую тройку.

 

 

Векторное произведение обозначается

Свойства векторного произведения:

1.

2.

3.

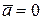4. ( или или 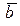=0).В частности:

Если векторы заданы своими координатами 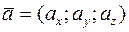, то

 

 

или